【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>![]() ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<![]() )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
参考答案:
【答案】(1) 抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;C(
x﹣2;C( ![]() ,﹣
,﹣![]() ).(2) ﹣1<m<0或3<m<4;(3)
).(2) ﹣1<m<0或3<m<4;(3)![]()
【解析】分析:(1)待定系数法求解析式即可,求得解析式后转换成顶点式即可.
(2)因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,所以-1<m<0,或3<m<4.
(3)左右平移时,使A′D+DB″最短即可,那么作出点C′关于x轴对称点的坐标为C″,得到直线P″C″的解析式,然后把A点的坐标代入即可.
详解:(1)∵抛物线y=ax2+bx﹣2(a≠0)过点A,B,
∴![]() ,
,
解得: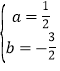 ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
∵y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴C(![]() ,﹣
,﹣![]() ).
).
(2)如图1,以AB为直径作圆M,则抛物线在圆内的部分,能使∠APB为钝角,
∴M(![]() ,0),⊙M的半径=
,0),⊙M的半径=![]() .
.
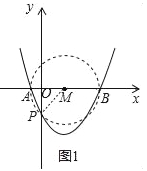
∵P′是抛物线与y轴的交点,
∴OP′=2,
∴MP′=![]() ,
,
∴P′在⊙M上,
∴P′的对称点(3,﹣2),
∴当﹣1<m<0或3<m<4时,∠APB为钝角.
(3)存在;
抛物线向左或向右平移,因为AB、P′C′是定值,所以A、B、P′、C′所构成的多边形的周长最短,只要AC′+BP′最小;
第一种情况:抛物线向右平移,AC′+BP′>AC+BP,
第二种情况:向左平移,如图2所示,由(2)可知P(3,﹣2),

又∵C(![]() ,﹣
,﹣![]() )
)
∴C'(![]() ﹣t,﹣
﹣t,﹣![]() ),P'(3﹣t,﹣2),
),P'(3﹣t,﹣2),
∵AB=5,
∴P″(﹣2﹣t,﹣2),
要使AC′+BP′最短,只要AC′+AP″最短即可,
点C′关于x轴的对称点C″(![]() ﹣t,
﹣t,![]() ),
),
设直线P″C″的解析式为:y=kx+b,
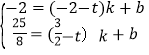 ,
,
解得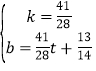
∴直线y=![]() ,
,
当P″、A、C″在一条直线上时,周长最小,
∴![]() =0
=0
∴t=![]() .
.
故将抛物线向左平移![]() 个单位连接A、B、P′、C′所构成的多边形的周长最短.
个单位连接A、B、P′、C′所构成的多边形的周长最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线
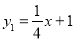 与
与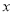 轴交于点
轴交于点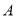 ,与
,与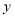 轴交于点
轴交于点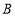 ,与反比例函
,与反比例函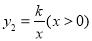 的图象交于点
的图象交于点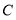 ,且
,且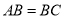 .
.(1)求点
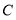 的坐标和反比例函数
的坐标和反比例函数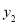 的解析式;
的解析式;(2)点
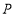 在
在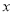 轴上,反比例函数
轴上,反比例函数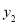 图象上存在点
图象上存在点 ,使得四边形
,使得四边形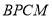 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.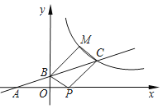
-
科目: 来源: 题型:
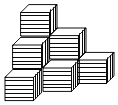
查看答案和解析>>【题目】棱长为a的正方体,摆放成如图所示的形状,动手试一试,并回答下列问题:
(1)如果这一物体摆放了如图所示的上下三层,由几个正方体构成?
(2)如图形所示物体的表面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应承办“绿色奥运”的号召,九年级(1)班全体师生义务植树300棵.原计划每小时植树x棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是( )
A.
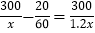 B.
B. 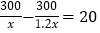
C.
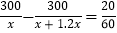 D.
D. 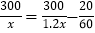
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,使点C落在点C′的位置,BC′交AD于点G(图1);再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M(图2),则EM的长为( )
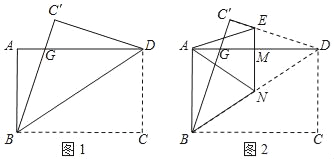
A. 2 B.
 C.
C. 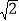 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场出售的A型冰箱每台售价2190元,每日耗电量为1度,而B型节能冰箱每台售价虽比A型冰箱高出10%,但每日耗电量却为0.55度,现将A型冰箱打折出售,商场最少打几折消费者购买才合算?(按使用期为10年,每年365天,每度电0.40元计算)
相关试题

