【题目】(本题满分10分)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由![]() 两工程队先后接力完成.
两工程队先后接力完成.![]() 工作队每天整治12米,
工作队每天整治12米,![]() 工程队每天整治8米,共用时20天.
工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
![]()
![]()
![]()
![]() 甲:
甲: ![]() 乙:
乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数![]() 表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:![]() 表示________________,
表示________________,![]() 表示_______________;
表示_______________;
乙:![]() 表示________________,
表示________________,![]() 表示_______________.
表示_______________.
(2)求![]() 两工程队分别整治河道多少米.(写出完整的解答过程)
两工程队分别整治河道多少米.(写出完整的解答过程)
参考答案:
【答案】(1)甲:![]() 表示
表示![]() 工程队工作的天数,
工程队工作的天数,![]() 表示
表示![]() 工程队工作的天数;
工程队工作的天数;
乙:![]() 表示
表示![]() 工程队整治河道的米数,
工程队整治河道的米数,![]() 表示
表示![]() 工程队整治河道的米数.
工程队整治河道的米数.

(2)解:设![]() 两工程队分别整治河道
两工程队分别整治河道![]() 米和
米和![]() 米,
米,
由题意得: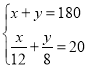
解方程组得:![]()
答:![]() 两工程队分别整治了60米和120米.
两工程队分别整治了60米和120米.
【解析】略
-
科目: 来源: 题型:
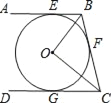
查看答案和解析>>【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
把代数式通过配凑等手段得到局部完全平方式,再进行有关计算和解题,这种解题方法叫做配方法.
如(1)用配方法分解因式:
 .
.解:原式=

=

(2)M=
 ,利用配方法求M的最小值.
,利用配方法求M的最小值.解:M=

=

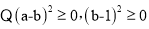
 M有最小值1.
M有最小值1.请根据上述材料,解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:

(2)用配方法分解因式:

(3)若M=
 ,求M的最小值.
,求M的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=60°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=2:3,则∠BEC的度数为_____.
相关试题

