【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
参考答案:
【答案】(1)1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;(2)2960.
【解析】
试题分析:(1)可设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,根据等量关系:①1辆甲种客车和3辆乙种客车共需租金1240元,②3辆甲种客车和2辆乙种客车共需租金1760元,列出方程组求解即可;
(2)由于求最节省的租车费用,可知租用甲种客车6辆,租用乙客车2辆,进而求解即可.
试题解析:(1)设1辆甲种客车的租金是x元,1辆乙种客车的租金是y元,依题意有:![]() ,解得:
,解得:![]() .
.
答:1辆甲种客车的租金是400元,1辆乙种客车的租金是280元;
(2)租用甲种客车6辆,租用乙客车2辆是最节省的租车费用,400×6+280×2=2400+560=2960(元).
答:最节省的租车费用是2960元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7)且与直线y=kx﹣2k﹣3相交于点P(m,2m﹣7).

(1)求抛物线的解析式;
(2)求直线y=kx﹣2k﹣3与抛物线y=ax2﹣(2a+1)x+b的对称轴的交点Q的坐标;
(3)在y轴上是否存在点T,使△PQT的一边中线等于该边的一半?若存在,求出点T的坐标;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.

(1)当α=60°时(如图1), ①判断△ABC的形状,并说明理由;
②求证:BD= AE;
AE;
(2)当α=90°时(如图2),求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
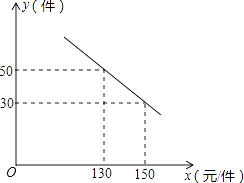
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论:w
①若a+b+c=0,且abc≠0,则方程a+bx+c=0的解是x=1;
②若a(x﹣1)=b(x﹣1)有唯一的解,则a≠b;
③若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=﹣
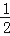 ;
;④若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解;
其中结论正确个数有( )
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=12cm,且
 ,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,△CPQ的周长为18cm,问:经过几秒后,△CPQ是等腰三角形?

相关试题

