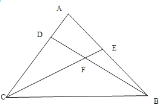
【题目】在△ABC中,∠ACB=60°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=2:3,则∠BEC的度数为_____.
参考答案:
【答案】100°;
【解析】
根据直角三角形的性质得∠BDC=90°,根据角平分线的性质得∠ECB=∠ECA =30°,再结合题意可以得到答案.
因为AC边上的高BD与CE所在的直线交于点F,
所以∠BDC=90°,
由∠ACB=60°,三角形内角和为180°,
可得∠DBC=180°-90°-60°=30°,
因为CE为△ABC的角平分线,
所以∠ECB=∠ECA =30°,
由∠ABD:∠ACF=2:3,且∠ECA=∠ACF =30°,
则∠ABD=20°,
则∠ABC=∠ABD+∠DBC=50°,
所以∠BEC=180°-∠DBC-∠ECB=100°,
故答案为100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由
 两工程队先后接力完成.
两工程队先后接力完成. 工作队每天整治12米,
工作队每天整治12米, 工程队每天整治8米,共用时20天.
工程队每天整治8米,共用时20天.(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:



 甲:
甲:  乙:
乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数
 表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:甲:
 表示________________,
表示________________, 表示_______________;
表示_______________;乙:
 表示________________,
表示________________, 表示_______________.
表示_______________.(2)求
 两工程队分别整治河道多少米.(写出完整的解答过程)
两工程队分别整治河道多少米.(写出完整的解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
把代数式通过配凑等手段得到局部完全平方式,再进行有关计算和解题,这种解题方法叫做配方法.
如(1)用配方法分解因式:
 .
.解:原式=

=

(2)M=
 ,利用配方法求M的最小值.
,利用配方法求M的最小值.解:M=

=

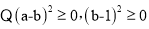
 M有最小值1.
M有最小值1.请根据上述材料,解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:

(2)用配方法分解因式:

(3)若M=
 ,求M的最小值.
,求M的最小值. -
科目: 来源: 题型:
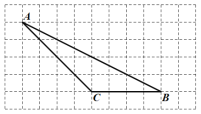
查看答案和解析>>【题目】如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校举办“大爱镇江”征文活动,小明为此次活动设计了一个以三座山为背景的图标(如图),现用红、黄两种颜色对图标中的A、B、C三块三角形区域分别涂色,一块区域只涂一种颜色.

(1)请用树状图列出所有涂色的可能结果;
(2)求这三块三角形区域中所涂颜色是“两块黄色、一块红色”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

相关试题

