【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.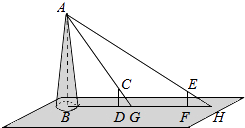
参考答案:
【答案】解:∵AB⊥BH,CD⊥BH,EF⊥BH,
∴AB∥CD∥EF,
∴△CDG∽△ABG,△EFH∽△ABH,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∵CD=DG=EF=2m,DF=52m,FH=4m,
∴ ![]() =
= ![]() ,
,
![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得BD=52,
∴ ![]() =
= ![]() ,
,
解得AB=54.
答:建筑物的高为54米
【解析】首先由AB∥CD∥EF可得出△CDG∽△ABG,△EFH∽△ABH,再根据相似三角形的对应边成比例列出比例式求解即可.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )
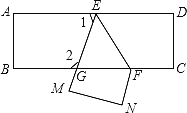
A. 115°B. 125°C. 135°D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一次函数
 的图象与
的图象与 轴交点坐标为
轴交点坐标为 ,如图所示.则下列说法:①
,如图所示.则下列说法:① 随
随 的增大而减小;②关于
的增大而减小;②关于 的方程
的方程 的解为
的解为 ;③
;③ 的解是
的解是 ;④
;④ .其中正确的说法有_____.(只填你认为正确说法的序号)
.其中正确的说法有_____.(只填你认为正确说法的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,∠2=2∠1,点C为x轴正半轴上的一动点.
(1)求∠1的度数;
(2)若OF∥AC,OE∥AB,求证:∠EOF=∠EAF;
(3)点C在运动中,若∠1=∠ACO,试判断AB与AC有怎样的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?

相关试题

