【题目】如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.

参考答案:
【答案】(1)2;(2)5;(3)见解析.
【解析】
(1)根据CD⊥AB即可进行判断;
(2)利用勾股定理求解即可;
(3)根据勾股定理可得BD2=BC2﹣CD2,AD2=AC2﹣CD2,再利用完全平方公式(AD+BD)2=AD2+2AD·BD+BD2,代入整理,根据勾股定理的逆定理即可得证.
(1)∵CD⊥AB,
∴△ACD与△BCD都是直角三角形,
故图中有2个直角三角形;
(2)在Rt△ACD中,
CD=![]() =5;
=5;
(3)在Rt△ACD中,AD2=AC2﹣CD2,
在Rt△BCD中,BD2=BC2﹣CD2,
∵CD2=AD·DB,
∴(AD+BD)2=AD2+2AD·BD+BD2
= AC2﹣CD2+2 CD2+BC2﹣CD2
= AC2+ BC2=AB2,
则△ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为倡导绿色出行,平阳县在昆阳镇设立了公共自行车服务站点,小明对某站点公共自行车的租用情况进行了调查,将该站点一天中市民每次租用公共自行车的时间t(单位:分)(t≤120)分成A,B,C,D四个组进行各组人次统计,并绘制了如下的统计图,请根据图中信息解答下列问题:

(1)该站点一天中租用公共自行车的总人次为 , 表示A的扇形圆心角的度数是 .
(2)补全条形统计图.
(3)考虑到公共自行车项目是公益服务,公共自行车服务公司规定:市民每次使用公共自行收费2元,已知昆阳镇每天租用公共自行车(时间在2小时以内)的市民平均有5000人次,据此估计公共自行车服务公司每天可收入多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图形中,所有四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形边长为7cm,设正方形A、B、C、D、E、F面积分别为SA、SB、SC、SD、SE、SF,则下列各式正确有()个.

① SA+SB+SC+SD=49;② SE+SF=49;③ SA+SB+SF=49;④ SC+SD+SE=4
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )
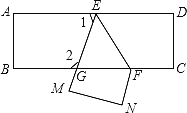
A. 115°B. 125°C. 135°D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一次函数
 的图象与
的图象与 轴交点坐标为
轴交点坐标为 ,如图所示.则下列说法:①
,如图所示.则下列说法:① 随
随 的增大而减小;②关于
的增大而减小;②关于 的方程
的方程 的解为
的解为 ;③
;③ 的解是
的解是 ;④
;④ .其中正确的说法有_____.(只填你认为正确说法的序号)
.其中正确的说法有_____.(只填你认为正确说法的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
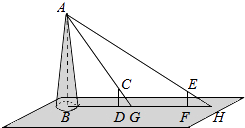
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,∠2=2∠1,点C为x轴正半轴上的一动点.
(1)求∠1的度数;
(2)若OF∥AC,OE∥AB,求证:∠EOF=∠EAF;
(3)点C在运动中,若∠1=∠ACO,试判断AB与AC有怎样的位置关系,并说明理由.

相关试题

