【题目】已知:四边形ABCD如图所示
(1)填空:∠A+∠B+∠C+∠D=______°
(2)请用两种方法证明你的结论。
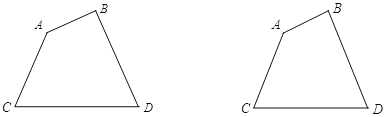
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】(1)∠A+∠B+∠C+∠D=![]() ,
,
(2)解法一:如图1,连接AC,
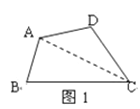
![]() ∠BAC+∠B+∠ACB=180°
∠BAC+∠B+∠ACB=180°
![]() ∠ACD+∠D+∠DAC=180°
∠ACD+∠D+∠DAC=180°
∴∠BAC+∠B+∠ACB+∠ACD+∠D+∠DAC=360°
∴∠DAC+∠B+∠BCD+∠D=360°
解法二:如图2,在四边形ABCD内取一点P,连接PA、PB、PC、PD
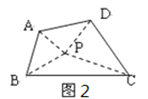
![]() ∠PAB+∠ABP+∠APB=180°
∠PAB+∠ABP+∠APB=180°
![]() ∠BPC+∠PBC+∠BCP=180°
∠BPC+∠PBC+∠BCP=180°
![]() ∠DPC+∠PCD+∠CDP=180°
∠DPC+∠PCD+∠CDP=180°
![]() ∠APD+∠ADP+∠DAP=180°
∠APD+∠ADP+∠DAP=180°
∴∠PAB+∠ABP+∠APB+∠BPC+∠PBC+∠BCP+∠DPC+∠PCD+∠CDP+∠APD+∠ADP +∠DAP=720°
∴∠DAC+∠ABC+∠BCD+∠ADC=360°
-
科目: 来源: 题型:
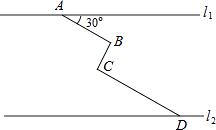
查看答案和解析>>【题目】如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(12a3﹣6a2+3a)÷3a﹣1;(2)因式分解:﹣3x3+6x2y﹣3xy2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
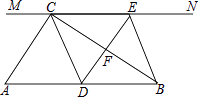
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若m,n都是正整数,且1≤n<m则下列按字母x的降幂排列是( )
A.xm+yn﹣2xy
B.yn+xm﹣2xy
C.xm﹣2xy+yn
D.yn﹣2xy+xm -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为_____________
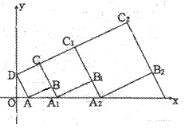
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象的大致形状是( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

