【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方2 ![]() 米处的点C出发,沿斜面坡度i=1:
米处的点C出发,沿斜面坡度i=1: ![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() .计算结果保留根号)
.计算结果保留根号)
参考答案:
【答案】解:如图,延长ED交BC延长线于点F,则∠CFD=90°,
∵tan∠DCF=i= ![]() =
= ![]() ,
,
∴∠DCF=30°,
∵CD=4,
∴DF= ![]() CD=2,CF=CDcos∠DCF=4×
CD=2,CF=CDcos∠DCF=4× ![]() =2
=2 ![]() ,
,
∴BF=BC+CF=2 ![]() +2
+2 ![]() =4
=4 ![]() ,
,
过点E作EG⊥AB于点G,
则GE=BF=4 ![]() ,GB=EF=ED+DF=1.5+2=3.5,
,GB=EF=ED+DF=1.5+2=3.5,
又∵∠AED=37°,
∴AG=GEtan∠AEG=4 ![]() tan37°,
tan37°,
则AB=AG+BG=4 ![]() tan37°+3.5=3
tan37°+3.5=3 ![]() +3.5,
+3.5,
故旗杆AB的高度为(3 ![]() +3.5)米
+3.5)米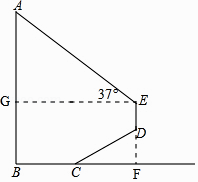
【解析】延长ED交BC延长线于点F,则∠CFD=90°,Rt△CDF中求得CF=CDcos∠DCF=2 ![]() 、DF=
、DF= ![]() CD=2,作EG⊥AB,可得GE=BF=4
CD=2,作EG⊥AB,可得GE=BF=4 ![]() 、GB=EF=3.5,再求出AG=GEtan∠AEG=4
、GB=EF=3.5,再求出AG=GEtan∠AEG=4 ![]() tan37°可得答案.
tan37°可得答案.
【考点精析】根据题目的已知条件,利用关于方向角问题的相关知识可以得到问题的答案,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)7﹣(﹣3)+(﹣5)
(2)﹣2.5÷

(3)﹣(﹣2)2﹣[(﹣6)2﹣4]
(4)

(5)3ab﹣4ab﹣(﹣2ab)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)2020年9月的日历如图1所示,用1×3的长方形框出3个数.如果任意圈出一横行左右相邻的三个数,设最小的数为x,用含x的式子表示这三个数的和为 ;如果任意圈出一竖列上下相邻的三个数,设最小的数为y,用含y的式子表示这三个数的和为
(2)如图2,用一个2×2的正方形框出4个数,是否存在被框住的4个数的和为96?如果存在,请求出这四个数中的最小的数字;如果不存在,请说明理由
(3)如图2,用一个3×3的正方形框出9个数,在框出的9个数中,记前两行共6个数的和为a1,最后一行3个数的和为a2.若|a1﹣a2|=6,请求出正方形框中位于最中心的数字m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图.A、B、C三点在格点上.
(1)作出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)在y轴上找点D,使得AD+BD最小,作出点D并写出点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=m时,多项式x2+2x+n2的值为﹣1,则x=﹣m时,该多项式的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产
 、
、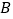 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件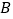 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.(1)设生产
 种产品
种产品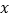 件,完成表格:
件,完成表格: 产品
产品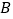 产品
产品生产数量(件
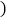
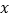 件
件件
需甲种原料(千克)
需乙种原料(千克)
(2)按要求安排
 、
、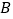 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.(3)以上方案哪种利润最大?是多少元?
相关试题

