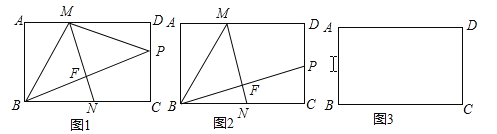
【题目】如图,将矩形纸片ABCD沿直线MN折叠,顶点B恰好与CD边上的动点P重合(点P不与点C,D重合),折痕为MN,点M,N分别在边AD,BC上,连接MB,MP,BP,BP与MN相交于点F.
(1)求证:△BFN∽△BCP;
(2)①在图2中,作出经过M,D,P三点的⊙O(要求保留作图痕迹,不写做法);
②设AB=4,随着点P在CD上的运动,若①中的⊙O恰好与BM,BC同时相切,求此时DP的长.
参考答案:
【答案】(1)证明见解析;(2)①作图见解析;②3.
【解析】
试题分析:(1)根据折叠的性质可知,MN垂直平分线段BP,即∠BFN=90°,由矩形的性质可得出∠C=90°=∠BFN,结合公共角∠FBN=∠CBP,即可证出△BFN∽△BCP;
(2)①在图2中,作MD、DP的垂直平分线,交于点O,以OD为半径作圆即可;
②设⊙O与BC的交点为E,连接OB、OE,由△MDP为直角三角形,可得出AP为⊙O的直径,根据BM与⊙O相切,可得出MP⊥BM,进而可得出△BMP为等腰直角三角形,根据同角的余角相等可得出∠PMD=∠MBA,结合∠A=∠PMD=90°、BM=MP,即可证出△ABM≌△DMP(AAS),根据全等三角形的性质可得出DM=AB=4、DP=AM,设DP=2a,根据勾股定理结合半径为直径的一半,即可得出关于a的方程,解之即可得出a值,再将a代入OP=2a中求出DP的长度.
试题解析:(1)证明:∵将矩形纸片ABCD沿直线MN折叠,顶点B恰好与CD边上的动点P重合,∴MN垂直平分线段BP,∴∠BFN=90°.
∵四边形ABCD为矩形,∴∠C=90°.
∵∠FBN=∠CBP,∴△BFN∽△BCP.
(2)解:①在图2中,作MD、DP的垂直平分线,交于点O,以OD为半径作圆即可.如图所示.
②设⊙O与BC的交点为E,连接OB、OE,如图3所示.
∵△MDP为直角三角形,∴AP为⊙O的直径,∵BM与⊙O相切,∴MP⊥BM.
∵MB=MP,∴△BMP为等腰直角三角形.
∵∠AMB+∠PMD=180°﹣∠AMP=90°,∠MBA+∠AMB=90°,∴∠PMD=∠MBA.
在△ABM和△DMP中,∵∠MBA=∠PMD,∠A=∠PMD=90°,BM=MP,∴△ABM≌△DMP(AAS),∴DM=AB=4,DP=AM.
设DP=2a,则AM=2a,OE=4﹣a,BM=![]() =
=![]() .
.
∵BM=MP=2OE,∴![]() =2×(4﹣a),解得:a=
=2×(4﹣a),解得:a=![]() ,∴DP=2a=3.
,∴DP=2a=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【感知】如图①,四边形ABCD、CEFG均为正方形.可知BE=DG. 【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习函数的经验,对函数y=
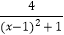 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题: 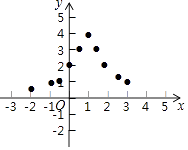
(1)函数y=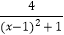 的自变量x的取值范围是
的自变量x的取值范围是
(2)表格是y与x的几组对应值.x
…
﹣2
﹣1
﹣

0

1

2

3
4
…
y
…
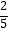
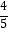
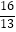
2
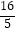
4
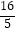
2
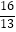

m
…
表中m的值为
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数y=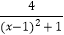 的大致图象;
的大致图象;
(4)结合函数图象,请写出函数y=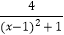 的一条性质:
的一条性质:
(5)如果方程 =a有2个解,那么a的取值范围是
=a有2个解,那么a的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
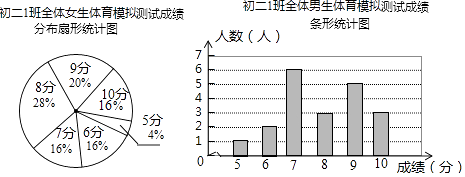
初二1班体育模拟测试成绩分析表平均分
方差
中位数
众数
男生
2
8
7
女生
7.92
1.99
8
根据以上信息,解答下列问题:
(1)这个班共有男生人,共有女生人;
(2)补全初二1班体育模拟测试成绩分析表; -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值(x-2)2+2(x+2)(x-4)-(x-3)(x+3);其中x=1.
-
科目: 来源: 题型:
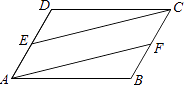
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E、F分别是AD、BC的中点.求证:AF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(a,b)在第四象限,则点C(-a-1,b-2)在第________象限
相关试题

