【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
参考答案:
【答案】(1)∵![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,
a=0有两个相等的实数根,
∴△=(![]() )2-4×
)2-4×![]() (c-
(c-![]() a)=0,
a)=0,
整理得a+b-2c="0" ①,
又∵3cx+2b=2a的根为x=0,
∴a="b" ②,
把②代入①得a=c,
∴a=b=c,
∴△ABC为等边三角形;
(2)a,b是方程x2+mx-3m=0的两个根,
∴方程x2+mx-3m=0有两个相等的实数根
∴△=m2-4×(-3m)=0,
即m2+12m=0,
∴m1=0,m2=-12.
当m=0时,原方程的解为x=0(不符合题意,舍去),
∴m=-12.
【解析】
(1)因为方程有两个相等的实数根,即△=0,由△=0可以得到一关于a,c的方程,再结合方程3cx+2b=2a的根为x=0,代入即可得到一关于a,b的方程,联立即可求出a,b,c的关系.
(2)根据(1)中求出a,b的值,可以关于m的方程,解方程即可求出m.
解:![]() ∵
∵![]() 有两个相等的5t实数根,
有两个相等的5t实数根,
∴![]() ,
,
整理得![]() ①,
①,
又∵![]() 的根为
的根为![]() ,
,
∴![]() ②,
②,
把②代入①得![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形;
为等边三角形;
![]() ,
,![]() 是方程
是方程![]() 的两个根,
的两个根,
∴方程![]() 有两个相等的实数根
有两个相等的实数根
∴![]() ,
,
即
∴![]() ,
,![]() .
.
当![]() 时,原方程的解为
时,原方程的解为![]() (不符合题意,舍去),
(不符合题意,舍去),
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明用三个等腰三角形(图中①②③)拼成了一个平行四边形ABCD,且
 ,则
,则 =_____ 度.
=_____ 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现场学习题:
问题背景:
在△ABC中,AB、BC、AC三边的长分别为
 、
、 、
、 ,求这个三角形的面积.
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上. .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法,若△ABC三边的长分别为
 a,2
a,2 a、
a、 a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .探索创新:
(3)若△ABC三边的长分别为
 、
、 、
、 (m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: . -
科目: 来源: 题型:
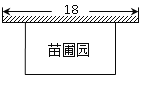
查看答案和解析>>【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图1、图2、图3,在
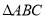 中,把
中,把 绕点
绕点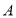 顺时针旋转
顺时针旋转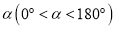 得到
得到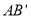 ,把
,把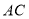 绕点
绕点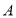 逆时针旋转
逆时针旋转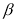 得到
得到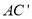 ,连接
,连接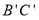 ,当
,当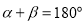 时,我们称
时,我们称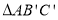 是
是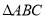 的“旋补三角形”,
的“旋补三角形”,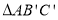 边
边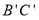 上的中线
上的中线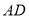 叫做
叫做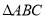 的“旋补中线”,点
的“旋补中线”,点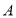 叫做“旋补中心”.图1、图2、图3中的
叫做“旋补中心”.图1、图2、图3中的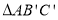 均是
均是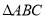 的“旋补三角形”.
的“旋补三角形”.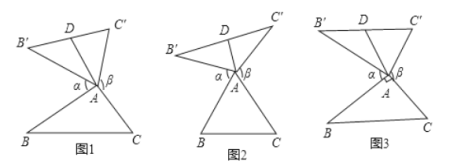
(1)①如图2,当
 为等边三角形时,“旋补中线”
为等边三角形时,“旋补中线”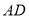 与
与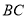 的数量关系为:
的数量关系为: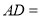 ______
______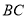 ;
;②如图3,当
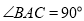 ,
,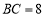 时,则“旋补中线”
时,则“旋补中线”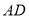 长为______.
长为______.(2)在图1中,当
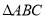 为任意三角形时,猜想“旋补中线”
为任意三角形时,猜想“旋补中线”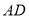 与
与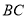 的数量关系,并给予证明.
的数量关系,并给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2
 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

相关试题

