搜索
【题目】如图，直线y=kx+b与双曲线
（x﹤0）相交于A（-4，a）、B（-1，4）两点.
（1）求直线和双曲线的解析式；
（2）在y轴上存在一点P，使得PA+PB的值最小，求点P的坐标.
参考答案：
【答案】（1）直线的解析式为y=x+5，双曲线的解析式为
；
（2）点P的坐标为
.
【解析】根据一次函数和反比例函数的解析式求出点A、B的坐标，然后作出点A关于y轴的对称点C，连接BC，与y轴的交点即为点P，然后求出直线BC的解析式，求出点P的坐标．
（1）y=x+5， 
；
（2）作点B关于y轴的对称点C（1，4），连接AC交y轴于点P.
易求得
，令x=0，得
，∴P
.
“点睛”本题考查了反比例函数与一次函数的交点问题，涉及了待定系数法求函数解析式、轴对称、最短路线问题，解答本题的关键是把两个函数关系式联立成方程组求出交点.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某企业积极响应政府“创新发展”的号召，研发了一种新产品．已知研发、生产这种产品的成本为30元/件，且年销售量y(万件)关于售价x(元/件)的函数解析式为：
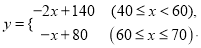
(1)若企业销售该产品获得的利润为W(万元)，请直接写出年利润W(万元)关于售价x(元/件)的函数解析式；
(2)当该产品的售价x(元/件)为多少时，企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元，试确定该产品的售价x(元/件)的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线
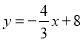与
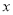轴，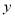 
轴分别交于点A、B，抛物线
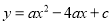经过点A和点B，与x轴的另一个交点为C，动点D从点A出发，以每秒1个单位长度的速度向O点运动，同时动点E从点B出发，以每秒2个单位长度的速度向A点运动，设运动的时间为t秒，0﹤t﹤5.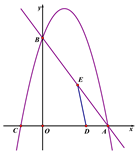
（1）求抛物线的解析式；
（2）当t为何值时，以A、D、E为顶点的三角形与△AOB相似；
（3）当△ADE为等腰三角形时，求t的值；
（4）抛物线上是否存在一点F，使得以A、B、D、F为顶点的四边形是平行四边形？若存在，直接写出F点的坐标；若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
ABCD中，AB=4，AD=7，∠ABC的平分线BE交AD于点E ， 则DE的长是（ ）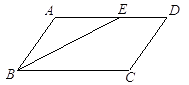
A.4
B.3
C.3.5
D.2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C、D是线段AB上两点，已知AC：CD：DB=1：2：3，M、N分别为AC、DB的中点，且AB=18cm．
（1）求线段CB的长；
（2）求线段MN的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】若一元二次方程x2﹣2x﹣1＝0的两个根为m、n，则一次函数y＝（m+n）x+mn的图象不经过（ ）
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目： 来源： 题型：
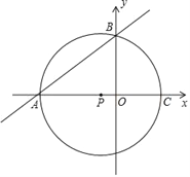
查看答案和解析>>【题目】如图，点A的坐标为（﹣8，0），点P的坐标为（-
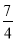，0），直线y=
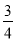x+b过点A，交y轴于点B，以点P为圆心，以PA为半径的圆交x轴于点C．（1）判断点B是否在⊙P上？说明理由．
（2）求过A、B、C三点的抛物线的解析式；并求抛物线与⊙P另外一个交点为D的坐标．
（3）⊙P上是否存在一点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．
相关试题
