搜索
【题目】如图，C、D是线段AB上两点，已知AC：CD：DB=1：2：3，M、N分别为AC、DB的中点，且AB=18cm．
（1）求线段CB的长；
（2）求线段MN的长．
参考答案：
【答案】
（1）解：设AC=x，则CD=2x，DB=3x，
∵AB=18cm，
∴x+2x+3x=18，
解得x=3，
∴CB=2x+3x=5x=5×3=15cm
（2）解：∵M、N分别为AC、DB的中点，∴AM=MC=1．5cm，DN=BN=4．5cm，∴MN=NC+CD+DN=1．5+6+4．5=12cm
【解析】（1）根据已知AC：CD：DB=1：2：3，因此设AC=x，则CD=2x，DB=3x，根据AC+CD+BD=18，建立方程求出x的值，就可得出CD、DB的长，然后根据CB=CD+DB，即可得出答案。
（2）根据中点的定义求出MC、DN的长，再根据MN=NC+CD+DN，就可求出答案。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线
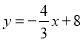与
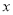轴，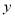 
轴分别交于点A、B，抛物线
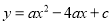经过点A和点B，与x轴的另一个交点为C，动点D从点A出发，以每秒1个单位长度的速度向O点运动，同时动点E从点B出发，以每秒2个单位长度的速度向A点运动，设运动的时间为t秒，0﹤t﹤5.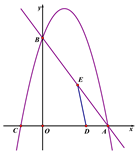
（1）求抛物线的解析式；
（2）当t为何值时，以A、D、E为顶点的三角形与△AOB相似；
（3）当△ADE为等腰三角形时，求t的值；
（4）抛物线上是否存在一点F，使得以A、B、D、F为顶点的四边形是平行四边形？若存在，直接写出F点的坐标；若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
ABCD中，AB=4，AD=7，∠ABC的平分线BE交AD于点E ， 则DE的长是（ ）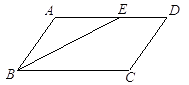
A.4
B.3
C.3.5
D.2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx+b与双曲线
（x﹤0）相交于A（-4，a）、B（-1，4）两点.
（1）求直线和双曲线的解析式；
（2）在y轴上存在一点P，使得PA+PB的值最小，求点P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一元二次方程x2﹣2x﹣1＝0的两个根为m、n，则一次函数y＝（m+n）x+mn的图象不经过（ ）
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目： 来源： 题型：
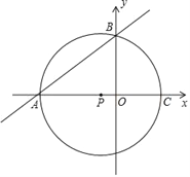
查看答案和解析>>【题目】如图，点A的坐标为（﹣8，0），点P的坐标为（-
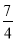，0），直线y=
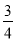x+b过点A，交y轴于点B，以点P为圆心，以PA为半径的圆交x轴于点C．（1）判断点B是否在⊙P上？说明理由．
（2）求过A、B、C三点的抛物线的解析式；并求抛物线与⊙P另外一个交点为D的坐标．
（3）⊙P上是否存在一点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面推理正确的是( )
A. ∵a∥b，b∥c，∴c∥d B. ∵a∥c，b∥d，∴c∥d
C. ∵a∥b，a∥c，∴b∥c D. ∵a∥b，c∥d，∴a∥c
相关试题
