【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点A、B,抛物线
轴分别交于点A、B,抛物线![]() 经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
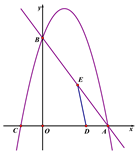
(1)求抛物线的解析式;
(2)当t为何值时,以A、D、E为顶点的三角形与△AOB相似;
(3)当△ADE为等腰三角形时,求t的值;
(4)抛物线上是否存在一点F,使得以A、B、D、F为顶点的四边形是平行四边形?若存在,直接写出F点的坐标;若不存在,说明理由.
参考答案:
【答案】(1)抛物线的解析式为![]() ;
;
(2)t的值为![]() 或
或![]() ;
;
(3)t的值为![]() 或
或![]() 或
或![]() ;
;
(4)符合条件的点F存在,共有两个![]() (4,8),
(4,8),![]() ,-8).
,-8).
【解析】(1)由B、C两点的坐标,利用待定系数法可求得抛物线的解析式;(2)利用△ADE∽△AOB和△AED∽△AOB即可求出t的值;(3)过E作EH⊥x轴于点H,过D作DM⊥AB于点M即可求出t的值;(4)分当AD为边时,当AD为对角线时符合条件的点F的坐标.
解:(1)A(6,0),B(0,8),依题意知![]() ,解得
,解得 ,
,
∴![]() .
.
(2)∵ A(6,0),B(0,8),∴OA=6,OB=8,AB=10,∴AD=t,AE=10-2t,
①当△ADE∽△AOB时, ![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
②当△AED∽△AOB时, ![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
综上所述,t的值为![]() 或
或![]() .
.
(3) ①当AD=AE时,t=10-2t,∴![]() ;
;
②当AE=DE时,过E作EH⊥x轴于点H,则AD=2AH,由△AEH∽△ABO得,AH=![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
③当AD=DE时,过D作DM⊥AB于点M,则AE=2AM,由△AMD∽△AOB得,AM=![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
综上所述,t的值为![]() 或
或![]() 或
或![]() .
.
(4) ①当AD为边时,则BF∥x轴,∴![]() ,求得x=4,∴F(4,8);
,求得x=4,∴F(4,8);
②当AD为对角线时,则![]() ,∴
,∴![]() ,解得
,解得![]() ,∵x﹥0,∴
,∵x﹥0,∴![]() ,∴
,∴![]() .
.
综上所述,符合条件的点F存在,共有两个![]() (4,8),
(4,8),![]() ,-8).
,-8).
“点睛”本题考查二次函数综合题、相似三角形等知识,解题的关键是学会待定系数法确定函数解析式,学会分类讨论,用方程的思想解决问题,属于中考压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△DEF,相似比为4:3,则△ABC与△DEF对应的中线之比为( )
A.4:3B.3:4C.16:9D.9:16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
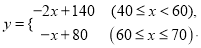
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD于点E , 则DE的长是( )
ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD于点E , 则DE的长是( )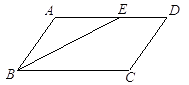
A.4
B.3
C.3.5
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b与双曲线
 (x﹤0)相交于A(-4,a)、B(-1,4)两点.
(x﹤0)相交于A(-4,a)、B(-1,4)两点.
(1)求直线和双曲线的解析式;
(2)在y轴上存在一点P,使得PA+PB的值最小,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=18cm.

(1)求线段CB的长;
(2)求线段MN的长.
相关试题

