【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
参考答案:
【答案】(1)年利润W(万元)关于售价x(元/件)的函数解析式为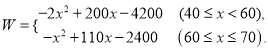 ;
;
(2)当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元;
(3)要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
【解析】(1)根据:年利润=(售价﹣成本)×年销售量,结合x的取值范围可列函数关系式;
(2)将(1)中两个二次函数配方后依据二次函数的性质可得其最值情况,比较后可得答案;
(3)根据题意知W≥750,可列关于x的不等式,求解可得x的范围.
解:(1) 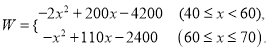
(2)由(1)知,当40≤x<60时, ![]() .
.
∵-2<0,∴当x=50时,W有最大值800.
当60≤x≤70时, ![]() .
.
∵-1<0, ∴当60≤x≤70时,W随x的增大而减小.
∴当x=60时,W有最大值600.
![]()
∴当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.
(3)当40≤x<60时,令W=750,得
-2(x-50)2+800=750,解之,得![]()
由函数![]() 的性质可知,
的性质可知,
当45≤x≤55时,W≥750.
当60≤x≤70时,W最大值为600<750.
所以,要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
“点睛”本题主要考查二次函数的实际应用,梳理题目中的数量关系,得出相等关系后分情况列出函数解析式,熟练运用二次函数性质求最值是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查红旗小学六年级学生的兴趣爱好,以下样本最具代表性的是( )
A. 该年级书法社团的学生 B. 该年级部分女学生
C. 该年级跑步较快的学生 D. 从每个班级中,抽取学号为10的整数倍的学生
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△DEF,相似比为4:3,则△ABC与△DEF对应的中线之比为( )
A.4:3B.3:4C.16:9D.9:16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
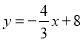 与
与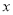 轴,
轴, 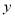 轴分别交于点A、B,抛物线
轴分别交于点A、B,抛物线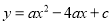 经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.
经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0﹤t﹤5.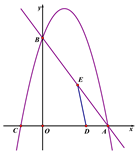
(1)求抛物线的解析式;
(2)当t为何值时,以A、D、E为顶点的三角形与△AOB相似;
(3)当△ADE为等腰三角形时,求t的值;
(4)抛物线上是否存在一点F,使得以A、B、D、F为顶点的四边形是平行四边形?若存在,直接写出F点的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD于点E , 则DE的长是( )
ABCD中,AB=4,AD=7,∠ABC的平分线BE交AD于点E , 则DE的长是( )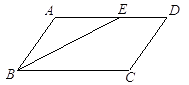
A.4
B.3
C.3.5
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b与双曲线
 (x﹤0)相交于A(-4,a)、B(-1,4)两点.
(x﹤0)相交于A(-4,a)、B(-1,4)两点.
(1)求直线和双曲线的解析式;
(2)在y轴上存在一点P,使得PA+PB的值最小,求点P的坐标.
相关试题

