搜索
【题目】若一元二次方程x2﹣2x﹣1＝0的两个根为m、n，则一次函数y＝（m+n）x+mn的图象不经过（ ）
A.第一象限B.第二象限C.第三象限D.第四象限
参考答案：
【答案】B
【解析】
利用根与系数的关系可得出m+n＝2，mn＝﹣1，结合一次函数图像与系数的关系可得出一次函数y＝（m+n）x+mn的图像经过第一、三、四象限，此题得解．
解：∵一元二次方程x2﹣2x﹣1＝0的两个根为m、n，
∴m+n＝2，mn＝﹣1，
∴一次函数y＝（m+n）x+mn＝2x－1的图像经过第一、三、四象限，不经过第二象限，
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
ABCD中，AB=4，AD=7，∠ABC的平分线BE交AD于点E ， 则DE的长是（ ）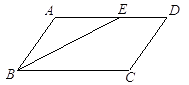
A.4
B.3
C.3.5
D.2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx+b与双曲线
（x﹤0）相交于A（-4，a）、B（-1，4）两点.
（1）求直线和双曲线的解析式；
（2）在y轴上存在一点P，使得PA+PB的值最小，求点P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C、D是线段AB上两点，已知AC：CD：DB=1：2：3，M、N分别为AC、DB的中点，且AB=18cm．
（1）求线段CB的长；
（2）求线段MN的长． -
科目： 来源： 题型：
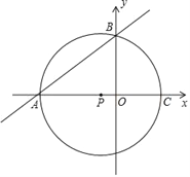
查看答案和解析>>【题目】如图，点A的坐标为（﹣8，0），点P的坐标为（-
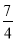，0），直线y=
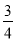x+b过点A，交y轴于点B，以点P为圆心，以PA为半径的圆交x轴于点C．（1）判断点B是否在⊙P上？说明理由．
（2）求过A、B、C三点的抛物线的解析式；并求抛物线与⊙P另外一个交点为D的坐标．
（3）⊙P上是否存在一点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面推理正确的是( )
A. ∵a∥b，b∥c，∴c∥d B. ∵a∥c，b∥d，∴c∥d
C. ∵a∥b，a∥c，∴b∥c D. ∵a∥b，c∥d，∴a∥c
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市为了增强学生体质，全面实施“学生饮用奶”营养工程．某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用．浠马中学为了了解学生对不同口味牛奶的喜好，对全校订购牛奶的学生进行了随机调查（每盒各种口味牛奶的体积相同），绘制了如图两张不完整的人数统计图：
（1）本次被调查的学生有 名；
（2）补全上面的条形统计图1，并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数；
（3）该校共有1200名学生订购了该品牌的牛奶，牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶．要使学生每天都喝到自己喜好的口味的牛奶，牛奶供应商每天送往该校的牛奶中，草莓味要比原味多送多少盒？
相关试题
