【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,E到C时两点同时停止运动。设点E运动的时间为ts(![]() ).
).
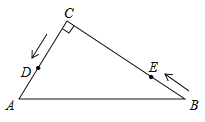
(1)AB=__________cm, CE=__________cm;
(2)当△BDE是直角三角形时,求t的值;
(3)若四边形CDEF是以CD、DE为一组邻边的平行四边形,
①设平行四边形CDEF的面积为Scm2,求S于t的关系式;
②是否存在某个时刻t,使□CDEF为菱形?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)10,8-t;(2)![]() 或
或![]() ;(3)①见解析,②存在,
;(3)①见解析,②存在, ![]() .
.
【解析】试题分析:(1)直接利用勾股定理进行求解;
(2)当△BDE是直角三角形时,∠B不可能为直角,所以分两种情况讨论:i)图1,当∠BED=90°时;ii)图2,当∠EDB=90°时;利用相似求边,从而求出t的值;
(3)①根据点D的位置分两种情况讨论:点D在边AC上时,0<t≤3;点D在边AB上时,3<t<8;CDEF的面积都等于△CDE面积的二倍;
②当CDEF为菱形,对角线CE和DF互相垂直且平分,利用BH=BE+EH列式计算.
试题解析:(1)由勾股定理得:AB=![]() =10;CE=8-t
=10;CE=8-t
(2)①如图1,

当∠BED=90°时,△BDE是直角三角形,
则BE=t,AC+AD=2t,
∴BD=6+10-2t=16-2t,
∵∠BED=∠C=90°,
∴DE∥AC,
∴![]() 即
即 ![]()
解得t=![]()
②如图2,当∠EDB=90°时,△BDE是直角三角形,则BE=t,BD=16-2t,
∴![]() 即
即![]()

解得t=![]()
(3)①如图3,

当0<t≤3时,BE=t,CD=2t,CE=8-t,
∴S□CDEF=2S△CDE= ![]() =
=![]() =
=![]() ,
,
如图4,当3<t<8时,BE=t,CE=8-t,过D作DH⊥BC,垂足为H,

∴S□CDEF=2S△CDE= ![]() =
=![]() =
=![]() ;
;
∴S于t的函数关系式为:当0<t≤3时,S=![]() ,当3<t<8时,S=
,当3<t<8时,S=![]() .
.
②存在,如图5,当□CDEF为菱形时,DH⊥CE,

由CD=DE得:CH=HE,
BH=![]() ,BE=t,EH=
,BE=t,EH=![]()
∴BH=BE+EH,即![]()
解得t=![]() ,
,
即当t=![]() 时,□CDEF为菱形.
时,□CDEF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是甲、乙两班参加“学法、用法知识竞赛”活动中各题答对人数的折线统计图,下列结论错误的是( )

A. 甲班答对第二题和第五题的人数相等
B. 甲班答对第三题的人数和乙班答对第三题的人数相等
C. 甲班答对第四题的人数比乙班答对第四题的人数少2人
D. 甲班答对各题的人数都比乙班的多
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克)
7
5
价格y(千克)
2000
4000
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B以及直线l,AE⊥l,垂足为点E.
(1)尺规作图:①过点B作BF⊥l,垂足为点F
②在直线l上求作一点C,使CA=CB;(要求:在图中标明相应字母,保留作图痕迹,不写作法)
(2)在所作的图中,连接CA、CB,若∠ACB=90°,∠CAE=
 ,则∠CBF= (用含
,则∠CBF= (用含 的代数式表示)
的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖。记每次抽出两张牌点数之差为x,按表格要求确定奖项.
奖项
一等奖
二等奖
三等奖
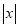
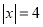
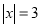
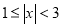
(1)用列表或画树状图的方法求出某同学抽一次奖获一等奖的概率;
(2)抽一次奖获一等奖的概率和不获奖的概率相等吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AC是□ABCD的一条对角线,过AC中点O的直线分别交AD、BC 于点E、F.

(1)求证:AE=CF;
(2)连接AF,CE.
①当EF⊥AC时,四边形AFCE是什么四边形?请证明你的结论;
②若AB=1,BC=2,∠B=60°,则四边形AFCE为矩形时,求EF的长.
相关试题

