【题目】AC是□ABCD的一条对角线,过AC中点O的直线分别交AD、BC 于点E、F.

(1)求证:AE=CF;
(2)连接AF,CE.
①当EF⊥AC时,四边形AFCE是什么四边形?请证明你的结论;
②若AB=1,BC=2,∠B=60°,则四边形AFCE为矩形时,求EF的长.
参考答案:
【答案】(1)证明见解析;(2)①菱形,证明见解析,②![]()
【解析】试题分析:(1)由平行四边形的性质可知OA=OC,∠AEO=∠OFC,∠EAO=∠OCF,证出△AOE≌△COF,即可得出AE=CF.
(2)①先证明四边形AFCE是平行四边形,由EF⊥AC,即可得出四边形AFCE是菱形;
②由矩形的性质得出EF=AC,∠AFB=∠AFC=90°,求出AF、CF,由勾股定理求出AC,即可得出EF的长.
试题解析:(1)∵O是AC中点
∴AO=C0
∵ABCD是平行四边形
∴AD∥BC
∴∠DAC=∠BCA
在ΔAOE和ΔCOF中
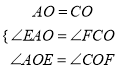
∴ΔAOE ≌ ΔCOF(ASA)
∴AE=CF
(2)①菱形
∵AE∥CF且AE=CF
∴AECF是平行四边形
∵AC⊥EF
∴AECF是菱形
②∵AECF是矩形
∴AF⊥BC
∵∠B=60°AB=1
∴BF=![]() AF=
AF=![]()
∵BC=2
∴FC=![]()
在RtΔAFC中AF=![]() FC=
FC=![]()
∴AC=![]()
又∵AFCE是矩形
∴EF=AC=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,E到C时两点同时停止运动。设点E运动的时间为ts(
 ).
).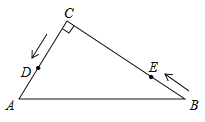
(1)AB=__________cm, CE=__________cm;
(2)当△BDE是直角三角形时,求t的值;
(3)若四边形CDEF是以CD、DE为一组邻边的平行四边形,
①设平行四边形CDEF的面积为Scm2,求S于t的关系式;
②是否存在某个时刻t,使□CDEF为菱形?若存在,求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B以及直线l,AE⊥l,垂足为点E.
(1)尺规作图:①过点B作BF⊥l,垂足为点F
②在直线l上求作一点C,使CA=CB;(要求:在图中标明相应字母,保留作图痕迹,不写作法)
(2)在所作的图中,连接CA、CB,若∠ACB=90°,∠CAE=
 ,则∠CBF= (用含
,则∠CBF= (用含 的代数式表示)
的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖。记每次抽出两张牌点数之差为x,按表格要求确定奖项.
奖项
一等奖
二等奖
三等奖
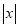
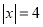
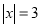
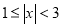
(1)用列表或画树状图的方法求出某同学抽一次奖获一等奖的概率;
(2)抽一次奖获一等奖的概率和不获奖的概率相等吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】淇淇和嘉嘉在学习了利用相似三角形测高之后分别测量两个旗杆高度.
(1)如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,已知淇淇同学的身高是1.54m,眼睛位置A距离淇淇头顶的距离是4cm,求旗杆DE 的高度.

如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为
 米,∠DCE=45°,求旗杆AB的高度?
米,∠DCE=45°,求旗杆AB的高度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(庆阳中考)现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了了解学生的视力变化情况,从全市九年级随机抽取了1 500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.

解答下列问题:
(1)图中D所在扇形的圆心角度数为______;
(2)若2016年全市共有30 000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
相关试题

