【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
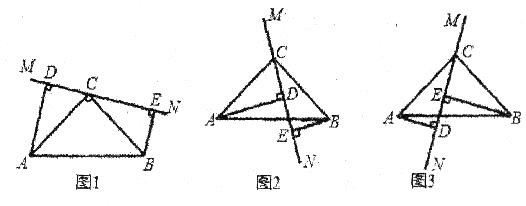
(1)①求证图1中△ADC≌△CEB;②证明DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE的理由;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由)。
参考答案:
【答案】(1)①详见解析;②详见解析;(2)DE =AD-BE,详见解析;(3)DE=BE![]()
【解析】
(1) 平角减去直角之后剩下的两个锐角互余是解题关键.证明△ADC≌△CEB即可;
(2) 直线分割直角所得的两个锐角互余,证明△ADC≌△CEB;
(3) 此小题和(2)解法一致.
(1)①如图1,在△ABC中,∠ACB=90°,![]() ,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,∠ADC=90°,∠BEC=90°,
,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,∠ADC=90°,∠BEC=90°,![]() ;因为
;因为![]() =90°,所以
=90°,所以![]() ,又因为AC=BC,所以△ADC≌△CEB,
,又因为AC=BC,所以△ADC≌△CEB,
②由①的结论知△ADC≌△CEB,所以CD=BE,AD=CE,所以
DE=CE+CD=AD+BE
(2)∵AD⊥MN于D,BE⊥MN于E
∴∠ADC=∠BEC=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°
∴∠CAD=∠BCE
在△ADC和△CEB中
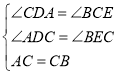
∴△ADC≌△CEB(AAS)
∴CE=AD,CD=BE
∴DE=CE-CD=AD-BE
(3)当MN旋转到图3的位置时,AD、DE、根据旋转的特征,结合(1)、(2)DE、AD、BE所满足的等量关系是DE=BE – AD(或AD=BE-DE,BE=AD+DE等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD=∠ABC,补充一个条件,使得△ABD≌△ABC,则下列选项不符合题意的是( )
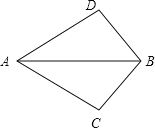
A. ∠D=∠CB. ∠DAB=∠CABC. BD=BCD. AD=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC<AB.若∠1、∠2分别为∠ABC、∠ACB的外角,则下列角度关系何者正确( )
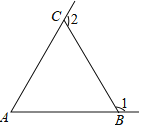
A.
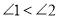
B.

C.
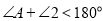
D.
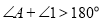
-
科目: 来源: 题型:
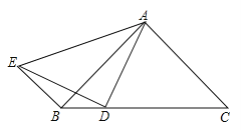
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB.
-
科目: 来源: 题型:
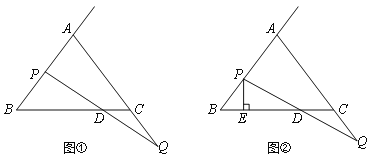
查看答案和解析>>【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为
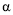 ,当
,当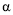 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2(x+1)﹣m=﹣
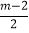 的解比方程5(x﹣1)﹣1=4(x﹣1)+1的解大2.
的解比方程5(x﹣1)﹣1=4(x﹣1)+1的解大2.(1)求第二个方程的解;
(2)求m的值.
相关试题

