搜索
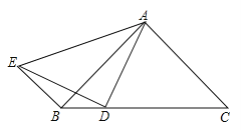
【题目】如图，在△ABC中，AB=AC，D是BC边上一点，连接AD，E为△ABC外一点，连接DE，AE和BE，AD=DE，BE∥AC.求证：∠BED=∠DAB.
参考答案：
【答案】见解析
【解析】
证明两角相等，可以通过证明全等三角形得到对应角相等，从而证明两角相等.此时要构造出全等三角形，构造全等三角形时，注意把已知的两组边相等AD=DE和两组所求的角相等∠BED=∠DAB，分别构造在同一个一个三角形中，一般作垂线构造直角三角形.构造出来直角三角形后，证明直角三角形可以用HL定理.此时只需要用角平分线的性质证明两个小直角边DM=DN即可.
证明：如图，作DN⊥AB，DM⊥BE，垂足分别为N，M，
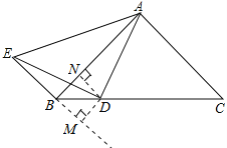
∵AB=AC，
∴∠ABC=∠C
∵BE∥AC，
∴∠C=∠DBM
∴∠NBD=∠MBD即BD平分∠ABM
∵DN⊥AB，DM⊥BE
∴DM=DN(角平分线上的点到角两边的距离相等)
在△AND和△EMD中 
∴Rt△AND≌Rt△EMD(HL)，
∠DAB=∠BED
-
科目： 来源： 题型：
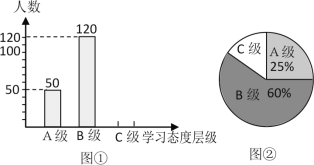
查看答案和解析>>【题目】初中生对待学习的态度一直是教育工作者关注的问题之一．为此某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了 名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计该市近20000名初中生中大约有多少名学生学习态度达标（达标包括A级和B级）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠ABD＝∠ABC，补充一个条件，使得△ABD≌△ABC，则下列选项不符合题意的是（ ）
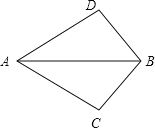
A. ∠D＝∠CB. ∠DAB＝∠CABC. BD＝BCD. AD＝AC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AC=BC＜AB.若∠1、∠2分别为∠ABC、∠ACB的外角，则下列角度关系何者正确（ ）
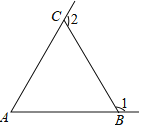
A.
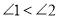
B.
C.
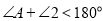
D.
-
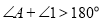
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。
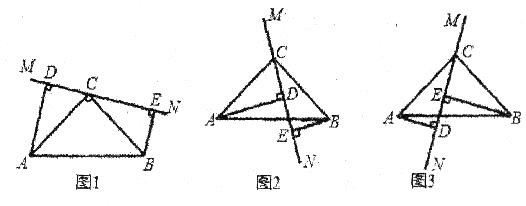
（1）①求证图1中△ADC≌△CEB；②证明DE=AD+BE；
（2）当直线MN绕点C旋转到图2的位置时，请说明DE=AD－BE的理由；
（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系（不必说明理由）。
-
科目： 来源： 题型：
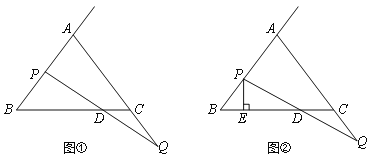
查看答案和解析>>【题目】已知△ABC中，AB＝AC＝BC＝6．点P射线BA上一点，点Q是AC的延长线上一点，且BP＝CQ，连接PQ，与直线BC相交于点D．
（1）如图①，当点P为AB的中点时，求CD的长；
（2）如图②，过点P作直线BC的垂线，垂足为E，当点P，Q分别在射线BA和AC的延长线上任意地移动过程中，线段BE，DE，CD中是否存在长度保持不变的线段？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC与△DCE有公共顶点C，AB=CD，BC=CE，∠ABC=∠DCE=90°.
（1）如图1，当点D在BC延长线上时.
①求证：△ABC≌△DCE.
②判断AC与DE的位置关系，并说明理由.
（2）如图2，△CDE从（1）中位置开始绕点C顺时针旋转，当点D落在BC边上时停止.
①若∠A=60°，记旋转的度数为
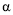，当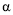为何值时，DE与△ABC一边平行.②如图3，若AB=c， BC=a， AC=b， a>c，边BC，DE交于点F，求整个运动过程中，F在BC上的运动路程（用含a， b， c的代数式表示）
相关试题
