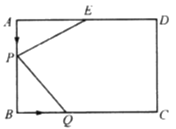
【题目】如图,在长方形![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 为
为![]() 的中点.若点
的中点.若点![]() 在线段
在线段![]() 上以1 cm/s的速度由点
上以1 cm/s的速度由点![]() 向点
向点![]() 运动,到点
运动,到点![]() 时不动.同时,点
时不动.同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.
运动.
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过1 s后,
的运动速度相等,经过1 s后,![]() 与
与![]() 是否全等?请说明理由,并判断此时线段
是否全等?请说明理由,并判断此时线段![]() 和
和![]() 的位置关系;
的位置关系;
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,运动时间为
的运动速度相等,运动时间为![]() s,设
s,设![]() 的面积为
的面积为![]() cm2,请用含
cm2,请用含![]() 的代数式表示
的代数式表示
(3)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
参考答案:
【答案】(1)见解析;(2)S=![]()
![]() t+6;(3)
t+6;(3)![]() cm/s
cm/s
【解析】
(1)本题很容易证明△AEP≌△BPQ,这样可得出∠AEP=∠BPQ,因为∠AEP+∠APE=90°,可得出∠BPQ+∠APE=90°,这即可判断出结论.
(2)可分别用t表示出AP、BQ、BP、CQ的长度,然后用矩形的面积减去△APE、△BPQ及梯形EDCQ的面积即可得出△PEQ的面积为Scm2.
(3)设Q运动的速度为xcm/s,则根据△AEP与△BQP得出AP=BP、AE=BQ或AP=BQ,AE=BP,从而可列出方程组,解出即可得出答案.
(1)∵长方形ABCD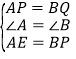 ,
,
∴∠A=∠B=90°,
∵点E为AD的中点,AD=6cm,
∴AE=3cm,
又∵P和Q的速度相等可得出AP=BQ=1cm,BP=3,
∴AE=BP,
在△AEP和△BQP中,
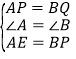 ,
,
∴△AEP≌△BPQ,
∴∠AEP=∠BPQ,
又∵∠AEP+∠APE=90°,
故可得出∠BPQ+∠APE=90°,即∠EPQ=90°,
即EP⊥PQ.
(2)连接QE,由题意得:AP=BQ=t,BP=4t,CQ=6t,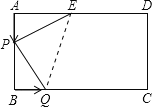
SPEQ=SABCDSBPQSEDCQSAPE=AD×AB![]() AE×AP
AE×AP![]() BP×BQ
BP×BQ![]() (DE+CQ)×CD=24
(DE+CQ)×CD=24![]() ×3t
×3t![]() t(4t)
t(4t) ![]() ×4(3+6t)=
×4(3+6t)= ![]()
![]() t+6,
t+6,
(3)设点Q的运动速度为xcm/s,
①经过y秒后,△AEP≌△BQP,则AP=BP,AE=BQ,
∴![]() ,
,
解得: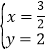 ,
,
即点Q的运动速度为![]() cm/s时能使两三角形全等.
cm/s时能使两三角形全等.![]()
②经过y秒后,△AEP≌△BPQ,则AP=BQ,AE=BP,
∴y=xy,3=4y,
解得: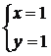 (舍去).
(舍去).
综上所述,点Q的运动速度为![]() cm/s时能使两三角形全等。
cm/s时能使两三角形全等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
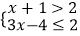 的解集表示在数轴上正确的是( )
的解集表示在数轴上正确的是( )
A.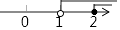
B.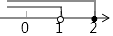
C.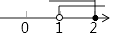
D.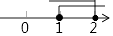
-
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,(1)∠AOC是哪两个角的和;(2)∠AOB是哪两个角的差;
(3)如果∠AOB=∠COD,那么∠AOC与∠DOB相等吗?
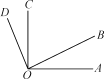
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中,其正确命题的个数是( ) ①若a>b,则
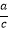 >
> 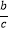 ;②垂直于弦的直径平分弦;③平行四边形的对角线互相平分;④反比例函数y=
;②垂直于弦的直径平分弦;③平行四边形的对角线互相平分;④反比例函数y= 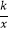 ,当k<0时,y随x的增大而增大.
,当k<0时,y随x的增大而增大.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 是等腰直角三角形,
是等腰直角三角形, ,点D是BC的中点
,点D是BC的中点 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG. 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______; 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转 ,
, 判断
判断 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论; 若
若 ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.
相关试题

