【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
参考答案:
【答案】解:(1)设年降水量为x万m3,每人年平均用水量为ym3,
由题意得,![]() ,解得:
,解得:![]() 。
。
答:年降水量为200万m3,每人年平均用水量为50m3.
(2)设该镇居民人均每年需节约z m3水才能实现目标,
由题意得,12000+25×200=20×25z,解得:z=34。
50﹣34=16m3.
答:设该镇居民人均每年需节约16 m3水才能实现目标。
(3)该企业n几年后能收回成本,
由题意得,![]() ,
,
解得:n≥![]() 。
。
答:至少9年后企业能收回成本。
【解析】(1)设年降水量为x万m3,每人年平均用水量为ym3,根据题意等量关系可得出方程组,解出即可。
(2)设该镇居民人均每年需节约z m3水才能实现目标,由等量关系得出方程,解出即可。
(3)该企业n年后能收回成本,根据投入1000万元设备,可得出不等式,解出即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+y)2=7,(x﹣y)2=3,则xy的值为( )
A.2B.1C.﹣1D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a>8),就站在A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人.
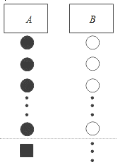
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少?(用含a的代数式表示)
(2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围.(不考虑其它因素)
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解答下列各题:
(1)解不等式:3x-5<2(2+3x);
(2)解不等式:2x-3≤
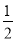 (x+2);
(x+2);(3)解不等式:
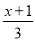 <x-1,并将解集在数轴上表示出来.
<x-1,并将解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按HUI图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2018个点的坐标为___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
相关试题

