搜索
【题目】平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2= ．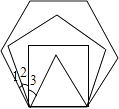 
参考答案：
【答案】24°
【解析】解：正三角形的每个内角是：
180°÷3=60°，
正方形的每个内角是：
360°÷4=90°，
正五边形的每个内角是：
（5﹣2）×180°÷5
=3×180°÷5
=540°÷5
=108°，
正六边形的每个内角是：
（6﹣2）×180°÷6
=4×180°÷6
=720°÷6
=120°，
则∠3+∠1﹣∠2
=（90°﹣60°）+（120°﹣108°）﹣（108°﹣90°）
=30°+12°﹣18°
=24°．
所以答案是：24°．
【考点精析】掌握多边形内角与外角和正多边形和圆是解答本题的根本，需要知道多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°；圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等．
-
科目： 来源： 题型：
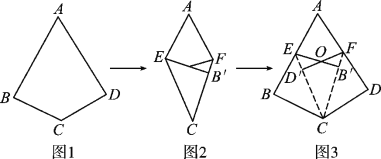
查看答案和解析>>【题目】阅读理解：如图1，如果四边形ABCD满足AB＝AD，CB＝CD，∠B＝∠D＝90°，那么我们把这样的四边形叫做“完美筝形”．将一张如图1所示的“完美筝形”纸片ABCD先折叠成如图2所示形状，再展开得到图3，其中CE，CF为折痕，∠BCE＝∠ECF＝∠FCD，点B′为点B的对应点，点D′为点D的对应点，连接EB′，FD′相交于点O.
简单应用：
(1)在平行四边形、矩形、菱形、正方形四种图形中，一定为“完美筝形”的是 ；
(2)当图3中的∠BCD＝120°时，∠AEB′＝ ；
拓展提升：
(3)当图2中的四边形AECF为菱形时，对应图3中的四边形CD′OB′是否是“完美筝形”？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
的面积是12，点D、E、F、G分别是BC、AD、BE、CE的中点，则四边形AFDG的面积是( ) 
A. 4.5B. 5C. 5.5D. 6
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰三角形ABC的底边BC在x轴正半轴上，点A在第一象限，延长AB交y轴负半轴于点D，延长CA到点E，使AE=AC，双曲线y=
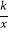（x＞0）的图象过点E．若△BCD的面积为2 
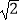，则k的值为（ ）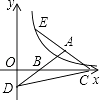
A.4
B.4
C.2
D.2 -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两车从A地开往B地，全程800km；所行的路程与时间的函数图像如图所示，下列问题：①乙车比甲车早出发2h；②甲车追上乙车时行驶了300km；③乙车的速度小于甲车速度；④甲车跑完全程比乙车跑完全程少用3h；以上正确的序号是_______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若三角形的一边和该边上的高相等的三角形称为“和谐三角形”，如图，已知抛物线y=ax2经过A（﹣1，1），P是y轴正半轴上的动点，射线AP与抛物线交于另一点B，当△AOP是“和谐三角形”时，点B的坐标为 ．
-
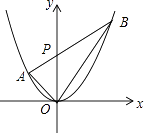
科目： 来源： 题型：
查看答案和解析>>【题目】综合与实践
某“综合与实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为
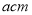的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒），请你动手操作验证并完成任务.（纸板厚度及接缝处忽略不计）动手操作一：
根据图1方式制作一个无盖的长方体盒子.方法：先在纸板四角剪去四个同样大小边长为
的小正方形，再沿虚线折合起来．
问题解决
（1）该长方体纸盒的底面边长为_______
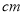；（请你用含
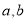的代数式表示）（2）若
，
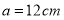，则长方体纸盒的底面积为_______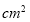
；动手操作二：
根据图2方式制作一个有盖的长方体纸盒．方法：先在纸板四角剪去两个同样大小边长为
的小正方形和两个同样大小的小长方形，再沿虚线折合起来．拓展延伸
（3）该长方体纸盒的体积为______
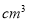；（请你用含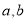的代数式表示）（4）现有两张边长
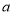均为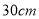
的正方形纸板，分别按图1、图2的要求制作无盖和有盖的两个长方体盒子，若
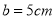，求无盖盒子的体积是有盖盒子体积的多少倍．
相关试题
