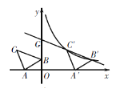
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(d,2).
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上. 请求出这个反比例函数和此时的直线B′C′的解析式.
参考答案:
【答案】(1)d=-3.(2)y=-![]() x+3.
x+3.
【解析】
(1)过C作CN垂直于x轴,交x轴于点N,由A、B及C的坐标得出OA,OB,CN的长,再证明Rt△CNA≌Rt△AOB,由∠CAB=90°,根据全等三角形的对应边相等可得出CN=0A,AN=0B,由AN+OA求出ON的长,再由C在第二象限,可得出d的值;
(2)由第一问求出的C与B的横坐标之差为3,根据平移的性质得到纵坐标不变,故设出C′(m,2),则B′(m+3,1),再设出反比例函数解析式,将C′与B′的坐标代入得到关于k与m的两方程,消去k得到关于m的方程,求出方程的解得到m的值,即可确定出k的值,得到反比例函数解析式,设直线B′C′的解析式为y=ax+b,将C′与B′的坐标代入,得到关于a与b的二元一次方程组,求出方程组的解得到a与b的值,即可确定出直线B′C′的解析式;
(1)如图,作CN⊥x轴于点N,
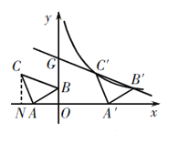
在Rt△CNA和Rt△AOB中,
CN=AO=2,AC=AB,
∴Rt△CNA≌Rt△AOB(HL),
则AN=BO=1,
∴NO=AN+AO=3,且点C在第二象限,
∴d=-3.
(2)设反比例函数为y=![]() ,点C′和B′在该反比例函数图象上,
,点C′和B′在该反比例函数图象上,
设C′(m-3,2),则B′(m,1),
把点C′和B′的坐标分别代入y=![]() ,
,
得k=2m-6,k=m,
∴m=2m-6,
则k=6,m=6,
反比例函数解析式为y=![]() .
.
得点C′(3,2),B′(6,1).
设直线C′B′的解析式为y=ax+b,
把C′、B′两点坐标代入得3a+b=2,6a+b=1,
∴解得a=-![]() ,b=3,
,b=3,
∴直线C′B′的解析式为y=-![]() x+3.
x+3.
-
科目: 来源: 题型:
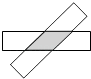
查看答案和解析>>【题目】如图,将两张长为4,宽为1的矩形纸条交叉并旋转,使重叠部分成为一个菱形.旋转过程中,当两张纸条垂直时,菱形周长的最小值是4,那么菱形周长的最大值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移
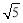 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+1与反比例函数y=
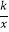 的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).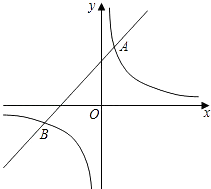
(1)求此反比例函数的解析式;
(2)当一次函数y=x+1的值大于反比例函数y=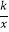 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 的长;
的长;
(Ⅱ)若 =
=  ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x
20
25
30
50
销售量y
15
12
10
6
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
相关试题

