【题目】如图,一次函数y=x+1与反比例函数y= ![]() 的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).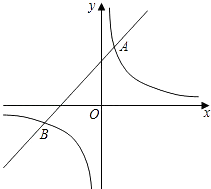
(1)求此反比例函数的解析式;
(2)当一次函数y=x+1的值大于反比例函数y= ![]() 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围.
参考答案:
【答案】
(1)解:∵A、B两点在一次函数y=x+1上,
∴a=1+1=2,﹣1=b+1,
∴b=﹣2,
∴A(1,2),B(﹣1,﹣2),
∵A点在反比例函数图象上,
∴k=1×2=2,
∴反比例函数解析式为y= ![]() ;
;
(2)解:当一次函数y=x+1的值大于反比例函数y= ![]() 的值时,即一次函数图象在反比例函数图象上方时所对应的x的取值范围,
的值时,即一次函数图象在反比例函数图象上方时所对应的x的取值范围,
∵A(1,2),B(﹣1,﹣2),
∴结合图象可知当一次函数y=x+1的值大于反比例函数y= ![]() 的值时,对应自变量x的取值范围为﹣1<x<0或x>1.
的值时,对应自变量x的取值范围为﹣1<x<0或x>1.
【解析】(1)根据题意,将点A、B两点坐标分别代入一次函数解析式求出a、b的值,即可求得点A、B的坐标,即可求出反比例函数的解析式。
(2)要求一次函数值大于反比例函数值,要看直线x-=1,直线x=-1,y轴,三条直线将两函数分成四部分,这四部分的自变量的取值范围分别是﹣1<x<0、x>1.x<-1,0<<1,此题可观察一次函数图象在反比例函数图象上方时所对应的x的取值范围,即可求解
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=1,点P1 , M1分别是AB,AC边的中点,点P2 , M2分别是AP1 , AM1的中点,点P3 , M3分别是AP2 , AM2的中点,按这样的规律下去,PnMn的长为(n为正整数).
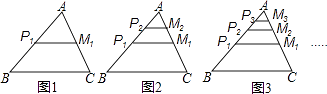
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两张长为4,宽为1的矩形纸条交叉并旋转,使重叠部分成为一个菱形.旋转过程中,当两张纸条垂直时,菱形周长的最小值是4,那么菱形周长的最大值是 .
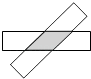
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移
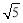 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论. -
科目: 来源: 题型:
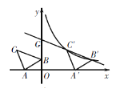
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(d,2).
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上. 请求出这个反比例函数和此时的直线B′C′的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 的长;
的长;
(Ⅱ)若 =
=  ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
相关试题

