【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
参考答案:
【答案】B
【解析】
把A(4,4)代入抛物线y=ax2+bx+3得4a+b=![]() ,根据对称轴x=-
,根据对称轴x=-![]() ,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,所以0<|2-(-
,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,所以0<|2-(-![]() )|≤1,解得a≥
)|≤1,解得a≥![]() 或a≤-
或a≤-![]() ,把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,得到a=
,把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,得到a=![]() -
-![]() ,所以
,所以![]() -
-![]() ≥
≥![]() 或
或![]() -
-![]() ≤-
≤-![]() ,即可解答.
,即可解答.
把A(4,4)代入抛物线y=ax2+bx+3得:
16a+4b+3=4,
∴16a+4b=1,
∴4a+b=![]() ,
,
∵对称轴x=![]() ,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,
,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,
∴0<|2(![]() )|≤1
)|≤1
∴0<|![]() |≤1,
|≤1,
∴|![]() |≤1,
|≤1,
∴a≥![]() 或a≤
或a≤![]() ,
,
把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,
2(2a+b)+3=m,
2(2a+![]() 4a)+3=m,
4a)+3=m,
![]() 4a=m,
4a=m,
a=![]() -
-![]() ,
,
∴![]() -
-![]() ≥
≥![]() 或
或![]() -
-![]() ≤-
≤-![]() ,
,
∴m≤3或m≥4.
故答案选:B.
-
科目: 来源: 题型:
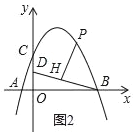
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=
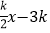 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.(1)求抛物线的解析式;
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
(3)在(2)的条件下,当d=
 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.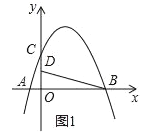
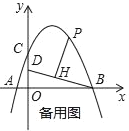
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=
 +bx+c经过A、B两点,与y轴交于点D(0,﹣6).
+bx+c经过A、B两点,与y轴交于点D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣
 ,y2)、点C(
,y2)、点C( ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确( )?

A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,﹣3),B(5,﹣1),C(1,3),结合所给的平面直角坐标系,解答下列问题:

(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于y轴对称的△A'B'C',并写出△A'B'C'各顶点坐标。
相关试题

