【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A、B两点,与y轴交于点D(0,﹣6).
+bx+c经过A、B两点,与y轴交于点D(0,﹣6).

(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)S=﹣
;(3)S=﹣![]() m2+
m2+![]() m+26(﹣2<m<4);(4)(
m+26(﹣2<m<4);(4)(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() )
)
【解析】
(1)先确定B(4,0),再利用待定系数法求出抛物线解析式为y=![]() ;
;
(2)先利用待定系数法求得直线AC的解析式为y=![]() x+
x+![]() ,则可确定E(0,
,则可确定E(0,![]() ),然后计算DE的长;
),然后计算DE的长;
(3)如图1,作PQ∥y轴交AC于Q,设P(m,![]() m2-
m2-![]() m-6),则Q(m,
m-6),则Q(m,![]() m+
m+![]() ),则PQ=-
),则PQ=-![]() m2+
m2+![]() m+
m+![]() ,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
,然后根据三角形面积公式,利用S=S△PAQ+S△PCQ计算即可;
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,根据角平分线的性质得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,则F(4,3),接着求出直线AF的解析式为y=![]() x+1,于是通过解方程组
x+1,于是通过解方程组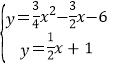 得N点坐标为(
得N点坐标为(![]() ,
,![]() );当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组
);当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组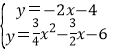 得N′的坐标.
得N′的坐标.
(1)∵BC⊥x轴,点C(4,8),
∴B(4,0),
把B(4,0),C(0,-6)代入y=![]() x2+bx+c得
x2+bx+c得
![]() ,解得
,解得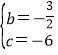 ,
,
∴抛物线解析式为y=![]() x2-
x2-![]() x-6;
x-6;
(2)设直线AC的解析式为y=px+q,
把A(-2,0),C(4,8)代入得
![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() x+
x+![]() =
=![]() ,则E(0,
,则E(0,![]() ),
),
∴DE=![]() +6=
+6=![]() ;
;
(3)如图1,作PQ∥y轴交AC于Q,
设P(m,![]() m2-
m2-![]() m-6),则Q(m,
m-6),则Q(m,![]() m+
m+![]() ),
),
∴PQ=![]() m+
m+![]() -(
-(![]() m2-
m2-![]() m-6)=-
m-6)=-![]() m2+
m2+![]() m+
m+![]() ,
,
∴S=S△PAQ+S△PCQ=![]() ×6×PQ=-
×6×PQ=-![]() m2+
m2+![]() m+26(-2<m<4);
m+26(-2<m<4);
(4)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,则FH=FB,
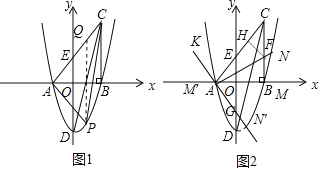
易得AH=AB=6,
∵AC=![]() ,
,
∴CH=10-6=4,
∵cos∠ACB=![]() ,
,
∴CF=![]() =5,
=5,
∴F(4,3),
易得直线AF的解析式为y=![]() x+1,
x+1,
解方程组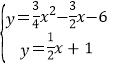 得
得![]() 或
或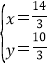 ,
,
∴N点坐标为(![]() ,
,![]() );
);
当点M′在x的负半轴上时,AN′交y轴与G,
∵∠CAN′=∠M′AN′,
∴∠KAM′=∠CAK,
而∠CAN=∠MAN,
∴∠KAC+∠CAN=90°,
而∠MAN+∠AFB=90°,
∴∠KAC=∠AFB,
而∠KAM′=∠GAO,
∴∠GAO=∠AFB,
∴Rt△OAG∽Rt△BFA,
∴![]() ,即
,即![]() ,解得OG=4,
,解得OG=4,
∴G(0,-4),
易得直线AG的解析式为y=-2x-4,
解方程组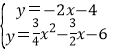 得
得![]() 或
或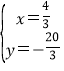 ,
,
∴N′的坐标为(![]() ,-
,-![]() ).
).
综上所述,满足条件的N点坐标为(![]() ,
,![]() ), (
), (![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=
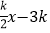 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.(1)求抛物线的解析式;
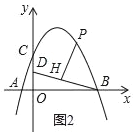
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
(3)在(2)的条件下,当d=
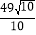 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.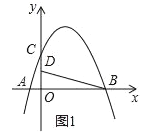
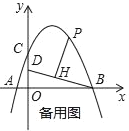
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣
 ,y2)、点C(
,y2)、点C( ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确( )?

A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确
相关试题

