【题目】一列快车和一列慢车同时从甲地出发,分别以速度v1、v2(单位:km/h,且v1>2v2)匀速驶向乙地.快车到达乙地后停留了2h,沿原路仍以速度v1匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.根据图象进行以下探究: 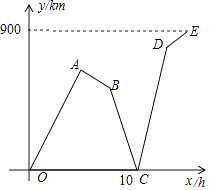
(1)甲、乙两地之间的距离为km;
(2)求线段AB、CD所表示的y与x之间的函数表达式;
(3)慢车出发多长时间后,两车相距480km?
参考答案:
【答案】
(1)900
(2)解:根据图象,得慢车的速度为 ![]() =60(km/h),
=60(km/h),
快车的速度为 ![]() =150(km/h),
=150(km/h),
所以线段AB所表示的y与x之间的函数表达式为y1=900﹣60x,
所以线段CD所表示的y与x之间的函数表达式为
y2=(60+150)(x﹣10)=210x﹣2100;
(3)解:①线段OA所表示的y与x之间的函数表达式为y3=90x(0≤x<6),
令y3=480,得x= ![]() ,
,
②线段AB所表示的y与x之间的函数表达式为y1=﹣60x+900(6≤x<8),
令y1=480,得x=7,
③线段CD所表示的y与x之间的函数表达式为y2=210x﹣2100(10≤x<14),
令y2=480,得x= ![]() .
.
答:慢车出发 ![]() h、7h、
h、7h、 ![]() h后,两车相距480km.
h后,两车相距480km.
【解析】(1)由图象即可得到结论;(2)根据图象,得到慢车的速度为 ![]() =60(km/h),快车的速度为
=60(km/h),快车的速度为 ![]() =150(km/h),于是得到结论;(3)根据每段的函数解析式即可得到结论.
=150(km/h),于是得到结论;(3)根据每段的函数解析式即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E.
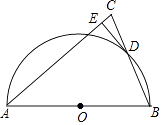
(1)求证:DE是⊙O的切线;
(2)若CE=1,BC=6,求半圆O的半径的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一组对边平行,另一组对边相等且不平行的四边形叫做等腰梯形.
(1)类比研究
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对四边形进行研究,完成表.四边形
对称性
边
角
对角线
平行
四边形.
两组对边分别平行,两组对边分别相等.
两组对角
分别相等.对角线互相平分.
等腰
梯形轴对称图形,过平行的一组对边中点的直线是它的对称轴.
一组对边平行,另一组对边相等.
.
.
(2)演绎论证
证明等腰梯形有关角和对角线的性质.
已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是对角线.
求证:
证明:
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系.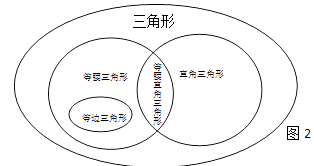
(3)请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c满足(a﹣7.5)2+
 +|c﹣8.5|=0.求:
+|c﹣8.5|=0.求:(1)a、b、c的值;
(2)求以a、b、c为边构成的三角形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2cm,BC=6cm,把△ABC沿对角线AC折叠,得到△AB′C,且B′C与AD相交于点E,则AE的长为cm.
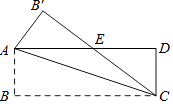
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD是角平分线,∠B=54°,∠C=76°.
(1)求∠ADB和∠ADC的度数;
(2)若DE⊥AC,求∠EDC的度数.
相关试题

