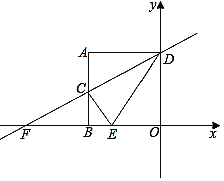
【题目】如图,A(-2,2)、AB⊥x轴于点B,AD⊥y轴于点D,C(-2,1)为AB的中点,直线CD交x轴于点F.
(1)求直线CD的函数关系式;
(2)过点C作CE⊥DF且交x轴于点E,求证:∠ADC=∠EDC;
(3)求点E坐标;
(4)点P是直线CE上的一个动点,求PB+PF的最小值.
参考答案:
【答案】(1)y=![]() x+2;(2)证明见解析;(3)E(
x+2;(2)证明见解析;(3)E(![]() ,0);(4)PB+PF的最小值为
,0);(4)PB+PF的最小值为![]() .
.
【解析】
(1)由题意先求出D的坐标,再利用待定系数法可求得直线CD的函数关系式;
(2)可先证明△ADC≌△BFC,利用全等三角形的性质得CF=CD,∠BFC=∠ADC,从而可证明DE=EF,最后利用等边对等角及等量代换即可证明∠ADC=∠EDC;
(3)利用直线CD的函数关系式可求出点F坐标,从而得到OF=4,设OE=x,则EF=DE=4-x,最后在Rt△DOE中利用勾股定理建立方程即可求出OE得到点E坐标;
(4)由(2)可知点D与F关于直线CE对称,连接BD交直线CE于点P,则可知P点即为满足条件的动点,由勾股定理可求得BD的长,即PB+PF的最小值.
解:(1)∵A(-2,2),AD⊥y轴于点D,
∴D(0,2),
设直线CD解析式为y=kx+b(k≠0),把点D(0,2),C(-2,1),代入得:![]() ,
,
解得![]() ,
,
∴直线CD的函数关系式为y=![]() x+2;
x+2;
(2)∵C是AB的中点,
∴AC=BC,
∵AD⊥y轴于点D,
∴AD∥x轴,
∵AB⊥x轴于点B,
∴∠A=∠CBF=90°,
在△ACD和△BCF中,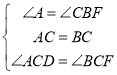 ,
,
∴△ACD≌△BCF(ASA),
∴CF=CD,∠BFC=∠ADC,
∵CE⊥DF,
∴CE垂直平分DF,
∴DE=FE,
∴∠EDC=∠EFC,
∴∠ADC=∠EDC;
(3)∵直线CD的函数关系式为y=![]() x+2,
x+2,
∴把y=0代入得0=![]() x+2,解得x=-4,
x+2,解得x=-4,
∴F(-4,0),
∴OF=4,
∵D(0,2),
∴OD=2,
设OE=x,则EF=DE=4-x,
在Rt△DOE中,![]() ,解得x=
,解得x=![]() ,即OE=
,即OE=![]() ,
,
∴E(![]() ,0);
,0);
(4)如图,连接BD交直线CE于点P,
由(2)可知点D与点F关于直线CE对称,
∴PD=PF,
∴PB+PF=PB+PD≥BD,
∵A(-2,2),AB⊥x轴于点B,
∴B(-2,0),
∴BD=![]() ,
,
∴PB+PF的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

-
科目: 来源: 题型:
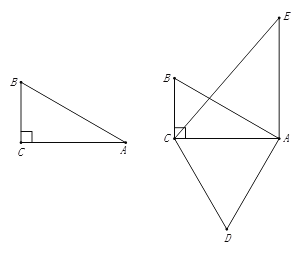
查看答案和解析>>【题目】如图1,直角三角形ABC中,∠C=90°,CB=1,∠BAC=30°.
(1)求AB、AC的长;
(2)如图2,将AB绕点A顺时针旋转60°得到线段AE,将AC绕点A逆时针旋转60°得到线段AD.
①连接CE,BD.求证:BD=EC;
②连接DE交AB于F,请你作出符合题意的图形并求出DE的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC·BC=BE·CD;
(2)已知CD=6、AD=3、BD=8,求⊙O的直径BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“”:观察下列各式:
23=2×3+3=9;3(﹣1)=3×3﹣1=8;
44=4×3+4=16:5(﹣3)=5×3﹣3=12
(1)请你想一想:ab= ;
(2)已知(a+3)2与|b﹣1|互为相反数,c与a互为倒数,试求c(ab)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,100个正方形由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最外面的正方形的边长为100cm,向里依次为99cm,98cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?
相关试题

