【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.

参考答案:
【答案】(1) CD2=AC·DB时,△ACP∽△PDB.
(2) 120°.
【解析】试题分析:(1)由△PCD是等边三角形可得∠ACP=∠PDB=120°,当![]() =
=![]() ,即
,即![]() =
=![]() ,即当CD2=AC·DB时,△ACP∽△PDB;(2)由△ACP∽△PDB可得∠A=∠DPB,所以∠APB=∠APC+∠CPD+∠DPB=∠APC+∠CPD+∠A=∠PCD+∠CPD=120°.
,即当CD2=AC·DB时,△ACP∽△PDB;(2)由△ACP∽△PDB可得∠A=∠DPB,所以∠APB=∠APC+∠CPD+∠DPB=∠APC+∠CPD+∠A=∠PCD+∠CPD=120°.
试题解析:
(1)∵△PCD是等边三角形,
∴∠ACP=∠PDB=120°.
当![]() =
=![]() ,即
,即![]() =
=![]() ,即当CD2=AC·DB时,△ACP∽△PDB.
,即当CD2=AC·DB时,△ACP∽△PDB.
(2)∵△ACP∽△PDB,∴∠A=∠DPB.
∴∠APB=∠APC+∠CPD+∠DPB=∠APC+∠CPD+∠A=∠PCD+∠CPD=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求四边形ABDC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.
(1)将△ABC向左平移7个单位长度后再向下平移3个单位长度,请画出经过两次平移后得到的△A1B1C1;
(2)以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1∶2.请在网格内画出在第三象限内的△A2B2C2,并写出点A2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别
成本价(元/箱)
销售价(元/箱)
甲
25
35
乙
35
48
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

-
科目: 来源: 题型:
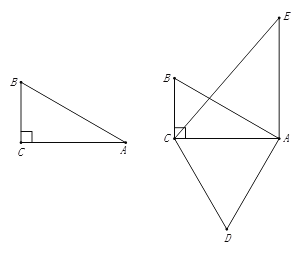
查看答案和解析>>【题目】如图1,直角三角形ABC中,∠C=90°,CB=1,∠BAC=30°.
(1)求AB、AC的长;
(2)如图2,将AB绕点A顺时针旋转60°得到线段AE,将AC绕点A逆时针旋转60°得到线段AD.
①连接CE,BD.求证:BD=EC;
②连接DE交AB于F,请你作出符合题意的图形并求出DE的长
-
科目: 来源: 题型:
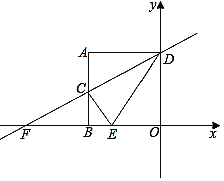
查看答案和解析>>【题目】如图,A(-2,2)、AB⊥x轴于点B,AD⊥y轴于点D,C(-2,1)为AB的中点,直线CD交x轴于点F.
(1)求直线CD的函数关系式;
(2)过点C作CE⊥DF且交x轴于点E,求证:∠ADC=∠EDC;
(3)求点E坐标;
(4)点P是直线CE上的一个动点,求PB+PF的最小值.
相关试题

