【题目】在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )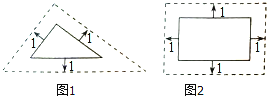
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
参考答案:
【答案】A
【解析】解答:甲:根据题意得:AB∥ ![]() ,AC∥
,AC∥ ![]() ,BC∥
,BC∥ ![]() , ∴∠A=∠
, ∴∠A=∠ ![]() ,∠B=∠
,∠B=∠ ![]() ,
,
∴△ABC∽△ ![]() ,
,
∴甲说法正确;
乙:∵根据题意得:AB=CD=3,AD=BC=5,则 ![]() =
= ![]() =3+2=5,
=3+2=5, ![]() =
= ![]() =5+2=7,
=5+2=7,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴新矩形与原矩形不相似.
∴乙说法正确.
故选:A.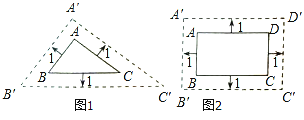
分析:甲:根据题意得:AB∥ ![]() ,AC∥
,AC∥ ![]() ,BC∥
,BC∥ ![]() ,可证得∠A=∠
,可证得∠A=∠ ![]() ,∠B=∠
,∠B=∠ ![]() ,由两角对应相等两三角形相似得△ABC∽△
,由两角对应相等两三角形相似得△ABC∽△ ![]() ;乙:根据题意得:AB=CD=3,AD=BC=5,则
;乙:根据题意得:AB=CD=3,AD=BC=5,则 ![]() =C′D′=3+2=5,A′D′=
=C′D′=3+2=5,A′D′= ![]() =5+2=7,则可得
=5+2=7,则可得 ![]() ,即新矩形与原矩形不相似.此题考查了相似三角形以及相似多边形的判定.
,即新矩形与原矩形不相似.此题考查了相似三角形以及相似多边形的判定.
【考点精析】解答此题的关键在于理解相似图形的相关知识,掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例,以及对相似三角形的判定的理解,了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC如图所示.则与△ABC相似的是图中的( )

A.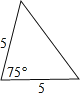
B.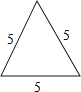
C.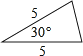
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
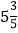 +(﹣
+(﹣ )+
)+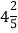 +(﹣
+(﹣ );
);(2)(
 ﹣
﹣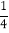 +
+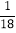 )÷(﹣
)÷(﹣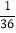 );
);(3)﹣15+(﹣2)3÷8﹣(﹣3)×
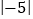 ;
;(4)﹣13÷(﹣5)2×
 +
+ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)将下列各数填在相应的大括号里:
﹣50%,2014,0.61,﹣3,﹣
 ,0,5.9,﹣3.14,﹣92
,0,5.9,﹣3.14,﹣92整数:{ ,… }
分数:{ ,… }
负分数:{ ,… }
(2)在(1)的数据中,最大的整数是 ,最小的分数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC , EF∥AB , 且S△ADE=4,S△EFC=9,则△ABC的面积为。
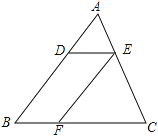
-
科目: 来源: 题型:
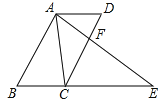
查看答案和解析>>【题目】如图,ABCD是平行四边形,点E在边BC延长线上,连AE交CD于点F , 如果∠EAC=∠D , 试问:ACBE与AECD是否相等?
相关试题

