搜索
【题目】如图，在四边形ABCD中，AB＝BC＝CD＝AD＝4，∠DAB＝∠B＝∠C＝∠D＝90°，E，F分别是边BC，CD上的点，且CE＝
BC，F为CD的中点，问△AEF是什么三角形？请说明理由.
参考答案：
【答案】直角三角形,理由见解析
【解析】
根据CE＝
BC，F为CD的中点，求出CE、CF、DF、BE的长，利用勾股定理求出EF2、AF2、AE2的长，利用勾股定理的逆定理判定即可.
∵AB＝BC＝CD＝AD＝4，CE＝BC，F为CD的中点
∴CE=1,CF=DF=2,BE=3
又∵∠DAB＝∠B＝∠C＝∠D＝90°
∴EF2=CE2+CF2=12+22=5 ,AF2=AD2+DF2=22+42=20 ,AE2=AB2+BE2=42+32=25
∵EF2+ AF2=5+20=25 =AE2
∴△AEF是直角三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】两个反比例函数
,
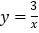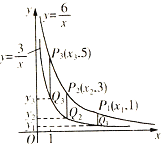
在第一象限内的图象如图所示，点P1，P2，P3，……P2005在反比例函数图象上，它们的横坐标分别是x1，x2，x3，x2005纵坐标分别为1，3，5，……；共2005个连续奇数，过点P1，P2，P3，……，P2005分别作
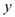轴的平行线，与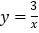的图象交点依次是Q1(x1，y1)，Q2（x2，y2），Q3(x3,y3)，……，Q2005（x2005，y2005）,则
_____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2），
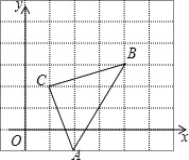
（1）写出点A、B的坐标：A（ ， ）、B（ ， ）
（2）将△ABC先向左平移1个单位长度，再向上平移2个单位长度，得到△A′B′C′，画出△A′B′C′
（3）写出三个顶点坐标A′（ 、 ）、B′（ 、 ）、C′ 、 ）
（4）求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）
（2）
.（3）-27+(-32)+(-8)+72 （4）
-
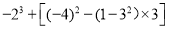
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在下面由火柴棒拼出的一系列的图形中，第n个图形由n个正方形组成．
（1）第2个图形中，火柴棒的根数是________；
（2）第3个图形中，火柴棒的根数是________；
（3）第4个图形中，火柴棒的根数是_______；
（4）第n个图形中，火柴棒的根数是_______ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠A＝∠ABC＝90°，AD＝1，BC＝3，点E是边CD的中点，连接BE并延长交AD的延长线于点F，连接CF．
(1)求证：四边形BDFC是平行四边形；
(2)若CB＝CD，求四边形BDFC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，点E是边AC上一点，线段BE垂直于∠BAC的平分线于点D，点M为边BC的中点，连接DM．
(1)求证: DM＝
CE； (2)若AD＝6，BD＝8，DM＝2，求AC的长．
相关试题
