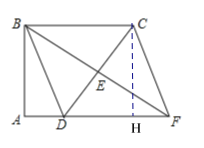
【题目】如图,在四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
(1)求证:四边形BDFC是平行四边形;
(2)若CB=CD,求四边形BDFC的面积.

参考答案:
【答案】(1)见解析 (2)3![]()
【解析】
(1)证明△BEC△FED,利用一组对边平行且相等的四边形是平行四边形即可判定.
(2)过C点作CH⊥AF,可证四边形ABCH为矩形,求得DH的长,利用勾股定理求出CH的长,利用平行四边形的面积公式即可求解.
(1)∵∠A=∠ABC=90°
∴BC∥AF
∴∠BCD=∠FDE,∠CBE=∠DFE
又∵点E是边CD的中点
∴CE=DE
∴△BCE△FDE(AAS)
∴BC=DF
又BC∥DF
∴四边形BDFC是平行四边形
(2) )过C点作CH⊥AF于H点.
则∠AHC=∠A=∠ABC=90°
∴四边形ABCH为矩形
∴AH=BC=3
∵AD=1
∴DH=2
又∵CB=CD
∴CD=3
根据勾股定理得:CH=![]()
∴S四边形BDFC=3![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 (2)
(2) .
.(3)-27+(-32)+(-8)+72 (4)
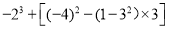
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E,F分别是边BC,CD上的点,且CE=
 BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在下面由火柴棒拼出的一系列的图形中,第n个图形由n个正方形组成.

(1)第2个图形中,火柴棒的根数是________;
(2)第3个图形中,火柴棒的根数是________;
(3)第4个图形中,火柴棒的根数是_______;
(4)第n个图形中,火柴棒的根数是_______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=
 CE;
CE; (2)若AD=6,BD=8,DM=2,求AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=
 或
或 .
.其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形
 中,
中,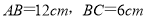 ,点
,点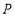 沿
沿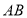 边从点
边从点 开始向点
开始向点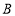 以
以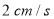 的速度移动,点
的速度移动,点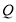 沿
沿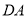 边从点
边从点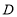 开始向点
开始向点 以
以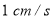 的速度移动,如果点
的速度移动,如果点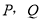 同时出发,用
同时出发,用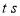 表示移动的时间(
表示移动的时间(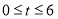 ).
).(1)当
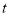 为何值时,
为何值时,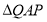 为等腰三角形?
为等腰三角形?(2)求四边形
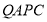 的面积,并探索一个与计算结果有关的结论.
的面积,并探索一个与计算结果有关的结论.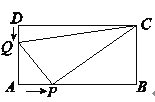
相关试题

