【题目】如图,在平面直角坐标系中,已知抛物线y=x2﹣bx+c经过A(0,3),B(1,0)两点,顶点为M. 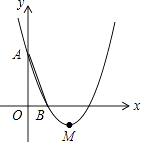
(1)则b= , c=;
(2)将△OAB绕点B顺时针旋转90°后,点A落到点C的位置,该抛物线沿y轴上下平移后经过点C,求平移后所得抛物线的表达式.
参考答案:
【答案】
(1)4;3
(2)解:∵A(0,3),B(1,0),
∴OA=3,OB=1.
∴旋转后C点的坐标为(4,1).
当x=4时,y=x2﹣4x+3=42﹣4×4+3=3,
∴抛物线y=x2﹣4x+3经过点(4,3).
∴将原抛物线沿y轴向下平移2个单位后过点C.
∴平移后的抛物线解析式为y=x2﹣4x+1
【解析】解:(1)已知抛物线y=x2﹣bx+c经过A(0,3),B(1,0)两点,∴ ![]() 解得:
解得: ![]() ,∴b、c的值分别为4,3.故答案是:4;3.
,∴b、c的值分别为4,3.故答案是:4;3.
【考点精析】本题主要考查了二次函数图象的平移的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣
 x2+
x2+  x+
x+  ,铅球运行路线如图.
,铅球运行路线如图. 
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,△ABC中,∠A=60,BD,CE是△ABC的两条角平分线,BD,CE相交于点O,求证:BC=CD+BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.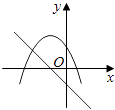
B.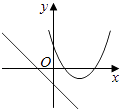
C.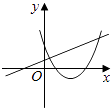
D.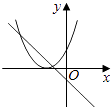
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a﹣b+c>0,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣
 ,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号)
,y2)在该图象上,则y1>y2 , 其中正确的结论是 . (填入正确结论的序号) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当方法解下列方程.
(1)x2﹣6x+5=0;
(2)2x2+3x﹣5=0.
相关试题

