【题目】一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,铅球运行路线如图.
,铅球运行路线如图. 
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m?
参考答案:
【答案】
(1)解:当y=0时,﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =0,
=0,
解之得x1=10,x2=﹣2(不合题意,舍去),
所以推铅球的水平距离是10米
(2)解:y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x2﹣8x+16﹣16)+
(x2﹣8x+16﹣16)+ ![]() =﹣
=﹣ ![]() (x2﹣8x+16)+
(x2﹣8x+16)+ ![]() +
+ ![]()
=﹣ ![]() (x﹣4)2+3,
(x﹣4)2+3,
当x=4时,y取最大值3,
所以铅球行进高度不能达到4m,最高能达到3m
【解析】(1)推出的水平距离就是当高度y=0时x的值,所以解方程可求解.(2)用配方法求解二次函数的最值即可判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为__度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,△ABC中,∠A=60,BD,CE是△ABC的两条角平分线,BD,CE相交于点O,求证:BC=CD+BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=x2﹣bx+c经过A(0,3),B(1,0)两点,顶点为M.
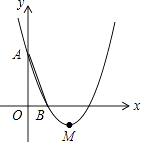
(1)则b= , c=;
(2)将△OAB绕点B顺时针旋转90°后,点A落到点C的位置,该抛物线沿y轴上下平移后经过点C,求平移后所得抛物线的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.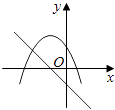
B.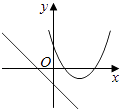
C.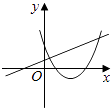
D.
相关试题

