【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)BE+CF>EF.理由见解析.
【解析】试题分析:(1)先利用ASA判定△BGD≌△CFD,从而得出BG=CF;
(2)再利用全等的性质可得GD=FD,再有DE⊥GF,从而得出EG=EF,两边和大于第三边从而得出BE+CF>EF.
试题解析:(1)∵BG∥AC,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
又∵∠BDG=∠CDF,
在△BGD与△CFD中,
∵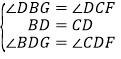
∴△BGD≌△CFD(ASA).
∴BG=CF.
(2)BE+CF>EF.
∵△BGD≌△CFD,
∴GD=FD,BG=CF.
又∵DE⊥FG,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究
(
 )如图①,已知正方形
)如图①,已知正方形 的边长为
的边长为 ,点
,点 和
和 分别是边
分别是边 、
、 上两点,且
上两点,且 .连接
.连接 和
和 ,交于点
,交于点 .猜想
.猜想 与
与 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.(
 )如图②,已知正方形
)如图②,已知正方形 的边长为
的边长为 ,点
,点 和
和 分别从点
分别从点 、
、 同时出发,以相同的速度沿
同时出发,以相同的速度沿 、
、 方向向终点
方向向终点 和
和 运动,连接
运动,连接 和
和 ,交于点
,交于点 ,求
,求 周长的最大值.
周长的最大值.问题解决
(
 )如图③,
)如图③, 为边长为
为边长为 的菱形
的菱形 的对角线,
的对角线,  .点
.点 和
和 分别从点
分别从点 、
、 同时出发;以相同的速度沿
同时出发;以相同的速度沿 、
、 向终点
向终点 和
和 运动,连接
运动,连接 和
和 ,交于点
,交于点 ,求
,求 周长的最大值.
周长的最大值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙ 的直径,
的直径,  是⊙
是⊙ 的切线,
的切线,  为切点,
为切点,  交⊙
交⊙ 于点
于点 .
.(Ⅰ)若
 为
为 的中点,证明:
的中点,证明:  是⊙
是⊙ 的切线.
的切线.(Ⅱ)若
 ,
,  ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有
 个白球、
个白球、 个蓝球;乙盒中有
个蓝球;乙盒中有 个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的
个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的 倍.
倍.(
 )求乙盒中蓝球的个数.
)求乙盒中蓝球的个数.(
 )从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
)从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 与
与 轴交于
轴交于 ,
,  两点,与
两点,与 轴交于点
轴交于点 .
.(
 )求抛物线的解析式.
)求抛物线的解析式.(
 )设抛物线的顶点为
)设抛物线的顶点为 ,点
,点 在抛物线的对称轴上,且
在抛物线的对称轴上,且 ,求点
,求点 的坐标.
的坐标.(
 )点
)点 在直线
在直线 上方的抛物线上,是否存在点
上方的抛物线上,是否存在点 使
使 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点 坐标.
坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四种沿
 折叠的方法中,不一定能判定纸带两条边线
折叠的方法中,不一定能判定纸带两条边线 ,
,  互相平行的是( ).
互相平行的是( ).
A. 如图
 ,展开后测得
,展开后测得
B. 如图
 ,展开后测得
,展开后测得
C. 如图
 ,测得
,测得
D. 如图
 ,展开后再沿
,展开后再沿 折叠,两条折痕的交点为
折叠,两条折痕的交点为 ,测得
,测得 ,
, 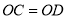
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个菱形绕着它的对角线的交点旋转
 ,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为
,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为 ,边长为
,边长为 ,则该“星形”的面积是__________.
,则该“星形”的面积是__________.
相关试题

