【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )
A.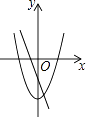
B.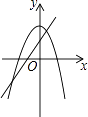
C.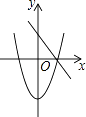
D.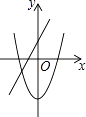
参考答案:
【答案】D
【解析】A、由直线y=ax+b的图象经过第二、三、四象限可知:a<0,b<0,
二次函数y=ax2﹣b的图象开口向上,∴a>0,A不正确,A不符合题意;
B、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向下,∴a<0,B不正确,B不符合题意;
C、由直线y=ax+b的图象经过第一、二、四象限可知:a<0,b>0,
二次函数y=ax2﹣b的图象开口向上,∴a>0,C不符合题意;
D、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向上,顶点在y轴负半轴,
∴a>0,b>0,D符合题意.
所以答案是:D.
【考点精析】掌握一次函数的图象和性质和二次函数的图象是解答本题的根本,需要知道一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批货物要运往某地,货主准备租用汽运公司的甲、乙两种货车,已知过去租用这两种汽车运货的情况如下表所示.
甲货车辆数
乙货车辆数
累计运货吨数
第一次
3
4
54
第二次
2
3
39
(1)一辆甲货车和一辆乙货车一次分别运货多少吨?
(2)若货主现有45吨货物,计划同时租用甲货车a辆,乙货车b辆,一次运完,且恰好每辆车都装满货物.
①请你帮助货主设计租车方案;
②若甲货车每辆租金200元,乙货车每辆租金240元.请选出省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.直线PE从B点出发,以2cm/s的速度向点A方向运动,并始终与BC平行,与AC交于点E.同时,点F从C点出发,以1cm/s的速度沿CB向点B运动,设运动时间为t (s)(0<t<5).
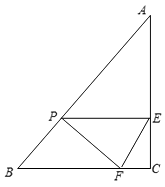
(1)当t为何值时,四边形PFCE是矩形?
(2)设△PEF的面积为S(cm2),求S与t的函数关系式;
(3)是否存在某一时刻t,使△PEF的面积是△ABC面积的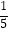 ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.
(4)连接BE,是否存在某一时刻t,使PF经过BE的中点?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
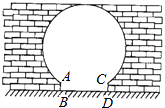
A.2米
B.2.5米
C.2.4米
D.2.1米 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是
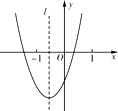
A.a<0
B.c>0
C.a+b+c>0
D.b2-4ac<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m<
 ;④n≤1.
;④n≤1.
则所有正确结论的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】(1计算:
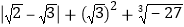 ;
;(2)解不等式组
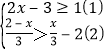
请结合题意填空,完成本题的解答:
解不等式(1),得______________.
解不等式(2),得_______________.
把不等式(1)和(2)的解集在数轴上表示出来

∴原不等式组的解集为_________________.
相关试题

