【题目】在平面直角坐标系中,点A(a,0)、B(b,0)(a≠0),a、b满足![]() +b2+2bc+c2=0
+b2+2bc+c2=0
(1) 直接写出a与b的关系
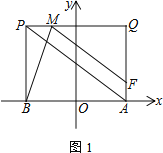
(2) 如图,将线段AB沿y轴的正方向平移m个单位得到线段PQ,点M在线段PQ上,QM=3MP,过M作MF∥PA交QA于点F,连接BM,BM平分∠PMF.若BM=![]() ,求m的值
,求m的值
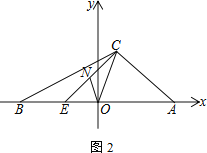
(3) 如图,点C在第一象限内,且满足CA=OA,点E在x轴上,AE=BC,连接CE,取CE的中点N,连接NO.若∠BCA=α,求∠NOC(用含α的代数式表示)
参考答案:
【答案】(1)a+b=0;(2)m=3;(3)∠NOC=90°-0.5ɑ
【解析】
(1)首先由题意,可得出![]() +
+![]() =0,进而可得出
=0,进而可得出![]() ;
;
(2)首先延长MF交x轴于F,得出MP,又因为MF∥PA,PM∥AH,得出四边形PMHA为平行四边形,进而得出AH和BH,又![]() ,即
,即![]() ,再根据BM平分∠PMF,即
,再根据BM平分∠PMF,即![]() ,得出
,得出![]() ,在Rt△PBA中,
,在Rt△PBA中,![]() ,即得出
,即得出
![]() ,即
,即![]() ,
,![]() ,在Rt△PBM中,
,在Rt△PBM中,![]() ,即
,即![]() ,将两个等式联立即可得出
,将两个等式联立即可得出![]() ;
;
(3)首先在OA上取一点F,使得OF=OE,连接CF,由BO=AO,EO=OF,BC=AE,得出BC=BF,进而得出∠BCF=∠BFC,又由N为CE的中点,即EO=OF,得出NO∥CF,进而得出∠NOC=∠OCF,又由∠BFC=∠FCA+∠FAC,∠BCO+∠OCF=∠BCF,得出∠FCA+∠FAC=∠BCO+∠OCF,又∠COA=∠BCO+∠CBO,将两式联立,得∠OCF=∠FCA+∠FAC-∠COA+∠CBO,又因为∠FAC+∠CBO=180°-α,得出∠OCF=180°-α-∠COA+∠FCA,又因为∠COA=∠OCF+∠FCA,得出∠OCF=90°-![]() ,即∠NOC=90°-
,即∠NOC=90°-![]() .
.
解:(1)由题意,得
![]() +b2+2bc+c2=0
+b2+2bc+c2=0
![]() +
+![]() =0
=0
∴![]()
∴![]()
(2)延长MF交x轴于F,如图所示
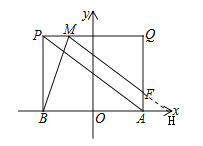
由题意得,P(b,m),Q(a,m)
又∵QM=3MP,
∴![]()
又∵MF∥PA,PM∥AH
∴四边形PMHA为平行四边形
∴![]() ,
,![]()
又![]() ,即
,即![]()
BM平分∠PMF,即![]()
∴![]() ,即
,即![]()
在Rt△PBA中,![]() ,
,![]() ,即
,即![]() ①
①
在Rt△PBM中,![]() ,即
,即
![]() ②
②
联立①②,解得
![]() .
.
(3)在OA上取一点F,使得OF=OE,连接CF,如图所示,
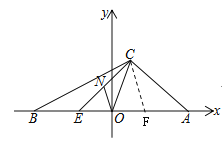
∵BO=AO,EO=OF,BC=AE,
∴BC=BF,
∴∠BCF=∠BFC,
又∵N为CE的中点,即EO=OF
∴NO∥CF
∴∠NOC=∠OCF
又∵∠BFC=∠FCA+∠FAC,∠BCO+∠OCF=∠BCF
∴∠FCA+∠FAC=∠BCO+∠OCF①
又∠COA=∠BCO+∠CBO②
①②联立,得∠OCF=∠FCA+∠FAC-∠COA+∠CBO
∵∠FAC+∠CBO=180°-α
∴∠OCF=180°-α-∠COA+∠FCA
又∵∠COA=∠OCF+∠FCA
∴∠OCF=90°-![]()
即∠NOC=90°-![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC为等腰三角形,AB=AC
(1) 作BD⊥AC于D,若CD=2,BD=4,求AB的长度
(2) 若AB=2,E为BC延长线上一点,且AE=4.若BC∶CE=2∶3,判断△ABE的形状,并证明结论


-
科目: 来源: 题型:
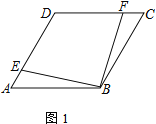
查看答案和解析>>【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
(1) 若AE=CF,求证:EB=BF
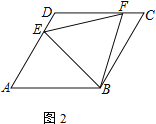
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
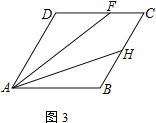
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】股民李明上星期六买进春兰公司股票1000股,每股27元.下表为本周内每日该股票的涨跌情况(单位:元)(注:本周一股票涨跌是在上周六的基础上,用正数记股价比前一日上升数,用负数记股价比前一日下降数)
星期
一
二
三
四
五
六
每股涨跌
+4
+4.5
-1
-2.5
-6
+2
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价每股多少元?
(3)己知李明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果李明在星期六收盘前将全部股票卖出,他的收益情况如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以矩形ABCD的边CD为直径作⊙O,交矩形的对角线BD于点E,点F是BC的中点,连接EF.
(1)试判断EF与⊙O的位置关系,并说明理由.
(2)若DC=2,EF=
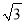 ,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)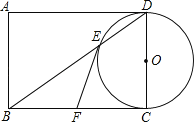
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段
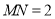 ,点
,点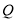 是线段
是线段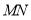 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.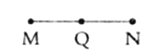
(1)延长线段
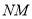 至点
至点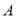 ,使
,使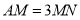 ;延长线段
;延长线段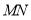 至点
至点 ,使
,使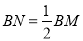 ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)(2)求线段
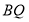 的长度;
的长度;(3)若点
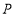 是线段
是线段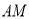 的中点,求线段
的中点,求线段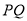 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题:
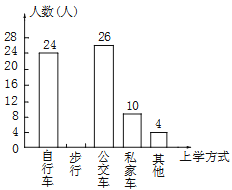
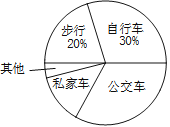
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
相关试题

