Question

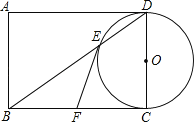
【题目】如图，以矩形ABCD的边CD为直径作⊙O，交矩形的对角线BD于点E，点F是BC的中点，连接EF．

（1）试判断EF与⊙O的位置关系，并说明理由．

（2）若DC=2，EF=，点P是⊙O上不与E、C重合的任意一点，则∠EPC的度数为 （直接写出答案）

Answer 1

【答案】（1）EF与⊙O相切，证明见解析；（2）600或1200

【解析】（1）直线EF与⊙O相切．理由如下：如图，连接OE、OF．通过△EFO≌△CFO（SAS），证得∠FEO=∠FCO=90°，则直线EF与⊙O相切．
（2）根据圆内接四边形的性质得到∠EPC+∠D=180°，利用（1）中的全等三角形的对应边相等求得FC=EF=，所以通过解直角△BCD来求∠D的度数即可．

解：（1）直线EF与⊙O相切．理由如下：
如图，连接OE、OF．

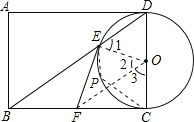
∵OD=OE，
∴∠1=∠D．
∵点F是BC的中点，点O是DC的中点，
∴OF∥BD，
∴∠3=∠D，∠2=∠1，
∴∠2=∠3．
∴在△EFO与△CFO中，

OE=OC，∠2=∠3，OF=OF，

∴△EFO≌△CFO（SAS），
∴∠FEO=∠FCO=90°，
∴直线EF与⊙O相切．

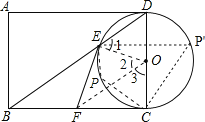
（2）如图，连接DF．
∵由（1）知，△EFO≌△CFO，
∴FC=EF=．
∴BC=2
在直角△FDC中，tan∠D==，
∴∠D=60°．

当点P在上时，
∵点E、P、C、D四点共圆，
∴∠EPC+∠D=180°，
∴∠EPC=120°．
当点P在 上时，

∠EPC=∠D=60°，

故填：60°或120°．
“点睛”本题考查了切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．