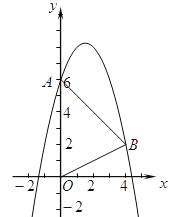
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求抛物线的解析式;
(2)将抛物线向下平移![]() 个单位,使平移后得到的抛物线顶点落在
个单位,使平移后得到的抛物线顶点落在![]() 的内部(不包括
的内部(不包括![]() 的边界),求
的边界),求![]() 的取值范围.
的取值范围.
(3)若![]() 是抛物线上一动点,是否存在点
是抛物线上一动点,是否存在点![]() ,使
,使![]() 的面积是
的面积是![]() ?若存在,直接写出P点坐标;若不存在,请说明理由.
?若存在,直接写出P点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 和
和![]()
【解析】
(1)把点A(0,6)、B(4,2)代入y=x2+bx+c,利用待定系数法即可得出抛物线的解析式;
(2)先利用配方法求出二次函数的顶点坐标,利用待定系数法分别求出直线AB与直线OB的解析式,将顶点横坐标的值分别代入两直线的解析式,求出对应的y的值,进而得出m的取值范围;
(3)设抛物线上存在点P(x,x2+3x+6),使△PAB的面积是10.过P作x轴的垂线,交直线AB于Q,则Q(x,x+6).分两种情况进行讨论:①点P在AB上方;②点P在AB下方.根据△PAB的面积是10列方程求解.
解:(1)抛物线过![]()
![]() ,
,![]() ,则有:
,则有:
![]()
解之得:![]()
∴所求的解析式是:![]()
(2)∵![]()
∴ 顶点的坐标为![]() .
.
设直线![]() 的解析式是
的解析式是![]() ,因为直线
,因为直线![]() 经过
经过![]() 、
、![]()
![]() 两点,
两点,
所以有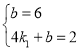 , 解之得:
, 解之得: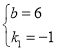
∴直线![]() 的解析式为
的解析式为![]() .
.
设直线![]() 的解析式是
的解析式是![]() ,因为直线
,因为直线![]() 经过
经过![]() 、
、![]()
![]() 两点,
两点,
所以有![]() ,解之得:
,解之得:![]()
∴直线![]() 的解析式为
的解析式为![]() .
.
把![]() 代入
代入![]() 得
得![]()
把![]() 代入
代入![]() 得
得![]()
∵![]() ,
,![]()
∴![]() .
.
(3)设抛物线上存在点P(x,x2+3x+6),使△PAB的面积是10.
过P作x轴的垂线,交直线AB于Q,
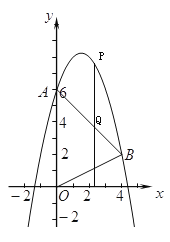
∵直线![]() 的解析式为
的解析式为![]() ,则Q(x,x+6).
,则Q(x,x+6).
分两种情况:①点P在AB上方时,
PQ=x2+3x+6(x+6)=x2+4x,
∵△PAB的面积=△PAQ的面积+△PQB的面积
=![]() PQ4=2PQ=10,
PQ4=2PQ=10,
∴PQ=5,
∴x2+4x=5,
解得x无实数根;
②点P在AB下方时,
PQ=(x+6)(x2+3x+6)=x24x,
∵△PAB的面积=|△PAQ的面积△PQB的面积|
=![]() PQ4=2PQ=10,
PQ4=2PQ=10,
∴PQ=5,
∴x24x=5,
解得x1=1,x2=5,
故所求P点坐标为(1,2)或(5,4).
综上,存在![]() 和
和![]() 使
使![]() 的面积是
的面积是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在家乡的楼顶上
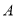 处测得池塘的一端
处测得池塘的一端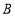 处的俯角为
处的俯角为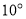 ,测得池塘
,测得池塘 处的俯角
处的俯角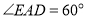 ,
,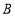 、
、 、
、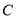 三点在同一水平直线上.已知楼高
三点在同一水平直线上.已知楼高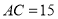 米,求池塘宽
米,求池塘宽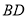 为多少米?(参考数据:
为多少米?(参考数据: ,
,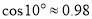 ,
, 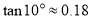 ,
,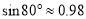 ,
,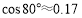 ,
, 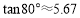 ,
,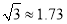 .结果保留一位小数.)
.结果保留一位小数.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年世界杯足球赛的“大力神杯”系列纪念品是中国制造.某商店用10000元购进一批“大力神杯”钥匙扣进行销售,很快销售一空.然后商店又用24000元购进这种钥匙扣,所购数量是第一批购进数量的2倍,但每个钥匙扣的价格比第一批的价格多了2元.
(1)该商店第一批购进的钥匙扣单价是多少元?
(2)若该商店第一、二批购进的钥匙扣都按相同的标价出售,并且全部售完,要使利润不低于20%,则每个钥匙扣的标价至少是多少元?
(3)在销售第二批钥匙扣时发现,若以每个15元价格出售,可全部售完.每涨价1元,销售量减少100件,剩余钥匙扣以每个10元价格全部售出.设该商店在销售第二批钥匙扣所获利润为P元,销售单价为m元,求P与m的函数关系式,并求出利润P最大时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
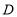 是⊙
是⊙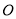 上一点,点
上一点,点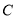 在直径
在直径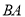 的延长线上,且
的延长线上,且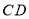 是⊙
是⊙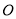 的切线,
的切线,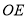 ∥
∥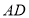 交
交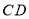 的延长线于点
的延长线于点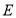 ,连结
,连结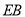 .
.(1) 求证:
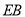 是⊙
是⊙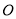 的切线.
的切线.(2) 若
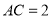 ,
,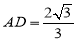 ,求⊙
,求⊙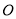 的半径.
的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两种糖果,原价分别为每千克a元和b元.根据调查,将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价下降15%,乙种糖果单价上涨20%,但按原比例混合的糖果单价恰好不变,则
 等于( )
等于( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点
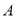 ,点
,点 在反比例函数
在反比例函数 的图象上,
的图象上,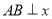 轴于点
轴于点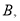 连结
连结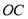 交
交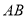 于点
于点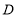 ,若
,若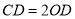 ,则
,则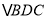 与
与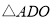 的面积比为( )
的面积比为( )
A.
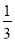 B.
B.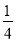 C.
C.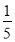 D.
D.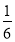
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出
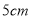 ,宽留出
,宽留出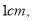 则该六棱柱的侧面积是( )
则该六棱柱的侧面积是( )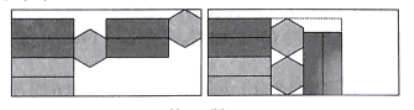
A.
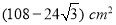 B.
B.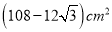
C.
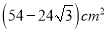 D.
D.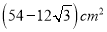
相关试题

