搜索
【题目】有甲、乙两种糖果，原价分别为每千克a元和b元．根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果．现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则
等于（ ）
A.
B.
C.
D.
参考答案：
【答案】D
【解析】
根据已知条件表示出价格变化前后两种糖果的平均价格，进而得出等式求出即可．
解：∵甲、乙两种糖果，原价分别为每千克a元和b元，
两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，
∴两种糖果的平均价格为：
，
∵甲种糖果单价下降15%，乙种糖果单价上涨20%，
∴两种糖果的平均价格为：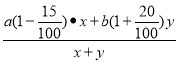
，
∵按原比例混合的糖果单价恰好不变，
∴＝，
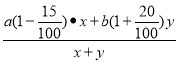整理，得
15ax＝20by
∴
，
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，正方形ABCD是由两个长为a、宽为b的长方形和两个边长分别为a、b的正方形拼成的．
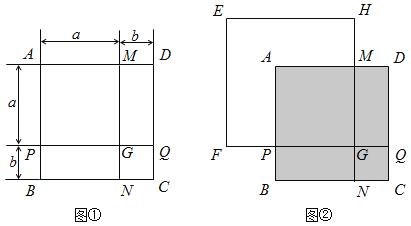
（1）利用正方形ABCD面积的不同表示方法，直接写出
、
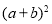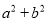、ab之间的关系式，这个关系式是 ；（2）若m满足
，请利用（1）中的数量关系，求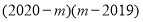
的值；（3）若将正方形EFGH的边
、
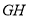分别与图①中的PG、MG重叠，如图②所示，已知PF=8，NH=32，求图中阴影部分的面积（结果必须是一个具体数值）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=
（n为常数，且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂足为D，若OB=2OA=3OD=12．（1）求一次函数与反比例函数的解析式；
（2）记两函数图象的另一个交点为E，求△CDE的面积；
（3）直接写出不等式kx+b≤
的解集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A是反比例函数y＝
在第一象限图象上一点，连接OA，过点A作AB∥x轴（点B在点A右侧），连接OB，若OB平分∠AOX，且点B的坐标是（8，4），则k的值是（ ）
A.6B.8C.12D.16
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图已知函数y=
（k＞0，x＞0）的图象与一次函数y=mx+5（m＜0）的图象相交不同的点A、B，过点A作AD⊥x轴于点D，连接AO，其中点A的横坐标为x0，△AOD的面积为2．（1）求k的值及x0=4时m的值；
（2）记[x]表示为不超过x的最大整数，例如：[1.4]=1，[2]=2，设t=ODDC，若﹣
＜m＜﹣
，求[m2t]值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB＝4，BC＝5，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE．延长AF交边BC于点G，则CG为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用适当的方法解下列方程：
(1)(6x－1)2＝25；
(2)x2－2x＝2x－1；
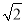(3)x2－
x＝2；(4)x(x－7)＝8(7－x)．
相关试题
