【题目】如图,在△ABC中,AB=AC,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.

(1)若∠BDA=115°,则∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
参考答案:
【答案】(1)25,115;(2)详见解析;(3)当∠BDA=110°或80°时,△ADE是等腰三角形.
【解析】
(1)根据三角形内角和定理,将已知数值代入即可求出∠BAD,根据平角为180°以及三角形内角和为180°即可算出∠DEC的度数;
(2)由条件可得∠EDC=∠DAB,∠B=∠C,DC=AB,根据ASA即可证明结论;
(3)若△ADE是等腰三角形,分为三种情况:①当AD=AE时,∠ADE=∠AED=40°,根据∠AED>∠C,得出此时不符合;②当DA=DE时,求出∠DAE=∠DEA=70°,求出∠BAC的度数,根据三角形的内角和定理求出∠BAD,根据三角形的内角和定理求出∠BDA即可;③当EA=ED时,求出∠DAC,求出∠BAD的度数,根据三角形的内角和定理求出∠BDA的度数.
(1)解:∵∠BDA=115°,∠B=40°,
∴∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
∵AB=AC,∠B=40°,
∴∠C=40°.
∵∠BDA+∠ADE+∠EDC=180°,∠ADE=40°,∠BDA=115°,
∴∠EDC=180°﹣115°﹣40°=25°.
∵∠EDC+∠C+∠DEC=180°,
∴∠DEC=180°﹣25°﹣40°=115°.
故答案为:25,115.
(2)证明:∵∠EDC+∠EDA+∠ADB=180°,∠DAB+∠B+∠ADB=180°,∠B=∠EDA=40°,
∴∠EDC=∠DAB.
∵∠B=∠C,DC=AB,
∴△ABD≌△DCE(ASA);
(3)解:∠BDA=80° 或∠BDA=110°.
∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠BDA=110°或80°时,△ADE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

解答下列问题:
(1)请用含
 、
、 、
、 的代数式表示大正方形的面积.
的代数式表示大正方形的面积.方法1: ;方法2: .
(2)根据图2,利用图形的面积关系,推导
 、
、 、
、 之间满足的关系式.
之间满足的关系式.(3)利用(2)的关系式解答:如果大正方形的面积是25,且
 ,求小正方形的面积.
,求小正方形的面积. -
科目: 来源: 题型:
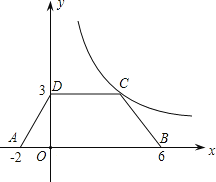
查看答案和解析>>【题目】如图,等腰梯形ABCD放置在平面坐标系中,已知A(﹣2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(1)求点C的坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:有一个长3米、宽2米、高4米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂蚁爬行的最短路径为( )
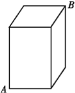
A.
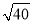 米B.
米B.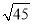 米C.
米C.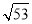 米D.
米D. 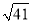 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的平分线,则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E, AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )cm.

A.9B.12C.15D.18
相关试题

