【题目】用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

解答下列问题:
(1)请用含![]() 、
、![]() 、
、![]() 的代数式表示大正方形的面积.
的代数式表示大正方形的面积.
方法1: ;方法2: .
(2)根据图2,利用图形的面积关系,推导![]() 、
、![]() 、
、![]() 之间满足的关系式.
之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且![]() ,求小正方形的面积.
,求小正方形的面积.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)1.
;(3)1.
【解析】
(1)方法1、根据正方形面积公式求出即可;
方法2、根据大正方形面积等于4个直角三角形面积加小正方形的面积,即可得出答案;
(2)根据大正方形面积相等,即可得出等式;
(3)由大正方形的面积是25可得![]() =25,利用完全平分公式,可得
=25,利用完全平分公式,可得![]() ,则2ab=24,根据小正方形的面积
,则2ab=24,根据小正方形的面积![]() ,即可解答.
,即可解答.
解:(1)方法1:大正方形的边长是![]() ,面积是
,面积是![]() ,
,
方法2:大正方形面积等于4个直角三角形面积加小正方形的面积,即![]() ;
;
(2)![]() =
=![]()
![]() =
=![]()
![]() ;
;
(3)∵正方形的面积是25,
∴![]() =25,
=25,
∵![]()
∴![]() ,2ab=24,
,2ab=24,
∴小正方形的面积:![]() =25-24=1.
=25-24=1.
故答案为:(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)1.
;(3)1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,点C的坐标为(1,0),∠ACB=90°,∠B=30°,当点A在反比例函数y=
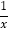 的图象上运动时,点B在函数_____(填函数解析式)的图象上运动.
的图象上运动时,点B在函数_____(填函数解析式)的图象上运动.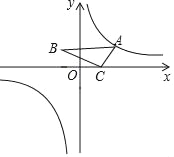
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
- 四边形ABCD是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

-
科目: 来源: 题型:
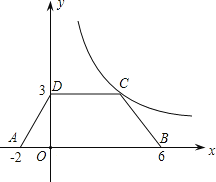
查看答案和解析>>【题目】如图,等腰梯形ABCD放置在平面坐标系中,已知A(﹣2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(1)求点C的坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.

(1)若∠BDA=115°,则∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:有一个长3米、宽2米、高4米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂蚁爬行的最短路径为( )
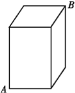
A.
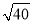 米B.
米B.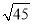 米C.
米C.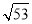 米D.
米D. 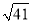 米
米
相关试题

