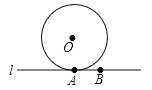
【题目】如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
(1)请用无刻度的直尺和圆规,过点B作直线m⊥l,交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)
(2)求BC的长.
参考答案:
【答案】(1)答案见解析;(2)2.
【解析】试题分析:(1)利用基本作图(过一点作已知直线的垂线)作直线m得到CD;
(2)作OH⊥CD于H,连接OA、OD,如图,利用垂径定理得到DH=CH,则根据切线的性质得OA⊥l,易得四边形OABH为正方形,所以OH=AB=4,BH=OA=5,然后利用勾股定理计算出DH=3,则CH=3,所以BC=BH﹣CH=2.
试题解析:解:(1)如图,CD为所作;
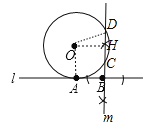
(2)作OH⊥CD于H,连接OA、OD,如图,则DH=CH.∵直线l切⊙O于A,∴OA⊥l,易得四边形OABH为正方形,∴OH=AB=4,BH=OA=5.在Rt△ODH中,DH=![]() =3,∴CH=3,∴BC=BH﹣CH=5﹣3=2.
=3,∴CH=3,∴BC=BH﹣CH=5﹣3=2.
-
科目: 来源: 题型:
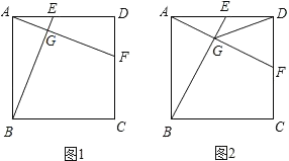
查看答案和解析>>【题目】如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
(1)写出BE与AF之间的关系,并证明你的结论;
(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(
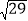 ,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.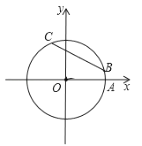
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形△ABC中,∠B=90°,AB=12cm,BC=16cm,点P从A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.P,Q分别从A,B同时出发,当一个动点到达终点则另一动点也随之停止运动.设运动时间为t(s)
(1)求t为何值时,△PBQ为等腰三角形?
(2)是否存在某一时刻t,使点Q在线段AC的垂直平分线上?
(3)点P、Q在运动的过程中,是否存在某一时刻t,直线PQ把△ABC的周长与面积同时分为1:2两部分?若存在,求出t,若不存在,请说明理由.
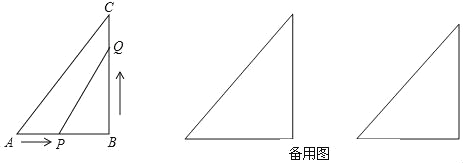
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点Q是CD边的中点,过点Q作AQ⊥PQ交BC于P,(1)证明:△ADQ ∽△QCP;(2)若PC=1,求BP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
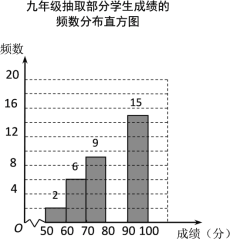
成绩x/分
频数
频率
第1段
x<60
2
0.04
第2段
60≤x<70
6
0.12
第3段
70≤x<80
9
b
第4段
80≤x<90
a
0.36
第5段
90≤x≤100
15
0.30
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)样本中,部分学生成绩的中位数落在第_______段;
(4)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A.
 B.
B.  C.
C.  D.
D. 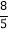
相关试题

