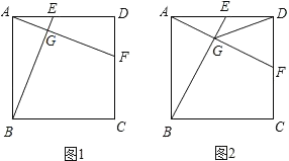
【题目】如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
(1)写出BE与AF之间的关系,并证明你的结论;
(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长.
参考答案:
【答案】(1)BE=AF,BE⊥AF,理由见解析;(2)证明见解析,GD=![]() .
.
【解析】
(1)根据正方形的性质可证△BAE≌△ADF(SAS),得到BE=AF,∠ABE=∠DAF,进而得出∠BGA=90°即可;
(2)先利用勾股定理求出AF,进而利用面积求出DN,判断出AG=DN,在判断出DM=AG,即可得出GD是∠MGN的平分线,进而判断△DGN是等腰直角三角形即可得出结论.
解:(1)BE=AF,BE⊥AF,理由:
四边形ABCD是正方形,
∴BA=AD=CD,∠BAE=∠D=90°,
∵DE=CF,
∴AE=DE,
∴△BAE≌△ADF(SAS),
∴BE=AF,∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAE+∠AEB=90°,
∴∠BGA=90°,
∴BE⊥AF;
(2)如图2,过点D作DN⊥AF于N,DM⊥BE交BE的延长线于M,
在Rt△ADF中,根据勾股定理得,AF=![]() ,
,
∵S△ADF=![]() AD×FD=
AD×FD=![]() AD×DN,
AD×DN,
∴DN=![]() ,
,
∵△BAE≌△ADF,
∴S△BAE=S△ADF,
∵BE=AF,
∴AG=DN,
又∵∠AGE=∠DME,∠AEG=∠DEM
∴△AEG≌△DEM(AAS),
∴AG=DM,
∴DN=DM,
∵DM⊥BE,DN⊥AF,
∴GD平分∠MGN,
∴∠DGN=![]() ∠MGN=45°,
∠MGN=45°,
∴△DGN是等腰直角三角形,
∴GD=![]() DN=
DN=![]() .
.

-
科目: 来源: 题型:
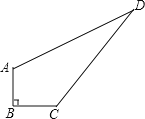
查看答案和解析>>【题目】为将我们的城市装扮的更美丽,园林绿化工人要将公园一角的一块四边形的空地ABCD种植上花草.经测量,∠B=90°,AB=3米,BC=4米,CD=12米,DA=13米.若每平方米空地需要购买150元的花草.将这块空地全部绿化需要购买多少元的这种花草?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100
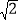 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据: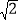 ≈1.41,
≈1.41,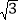 ≈1.73,计算结果保留两位小数)
≈1.73,计算结果保留两位小数)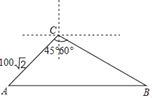
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.

(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(
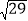 ,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.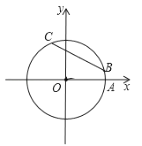
-
科目: 来源: 题型:
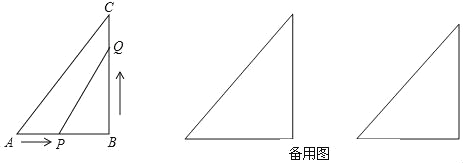
查看答案和解析>>【题目】如图,在直角三角形△ABC中,∠B=90°,AB=12cm,BC=16cm,点P从A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.P,Q分别从A,B同时出发,当一个动点到达终点则另一动点也随之停止运动.设运动时间为t(s)
(1)求t为何值时,△PBQ为等腰三角形?
(2)是否存在某一时刻t,使点Q在线段AC的垂直平分线上?
(3)点P、Q在运动的过程中,是否存在某一时刻t,直线PQ把△ABC的周长与面积同时分为1:2两部分?若存在,求出t,若不存在,请说明理由.
-
科目: 来源: 题型:
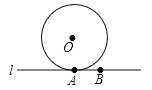
查看答案和解析>>【题目】如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
(1)请用无刻度的直尺和圆规,过点B作直线m⊥l,交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)
(2)求BC的长.
相关试题

