【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 的外接圆与边
的外接圆与边![]() 交于点
交于点![]() ,
,![]() ,
,
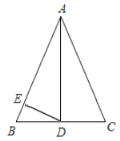
(1)①补全图形;②判断直线![]() 与
与![]() 的外接圆的公共点个数,并给出证明.
的外接圆的公共点个数,并给出证明.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
参考答案:
【答案】(1)①见解析;②1个,证明见解析;(2)3
【解析】
(1)①△ADC是直角三角形,则斜边AC的中点即为外接圆的圆心;
②利用等腰三角形ABC和等腰三角形ODC角度的关系,推导出∠ODE=90°,证OD与圆相切;
(2)如下图,连接CF,则DE是△BCF的中位线,在Rt△AFC中,利用三角函数关系表示出AF、FC、AC之间的长度关系,结合BE的长度可求得
(1)①图像如下,取AC的中点O,以OA为半径作圆,圆AB交于点F
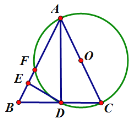
②如下图,连接OD
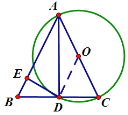
∵△ADC是直角三角形,点O是AC的中点
∴OA=OD=OC
∴∠ODC=∠OCD
∵AB=AC
∴∠ABC=∠ACB,∴∠ABC=∠ACB=∠ODC
∵DE⊥AB,∴∠BED=90°,∴∠EBD+∠EDB=90°
∴∠EDB+∠ODC=90°,∴∠EDO=90°
∴ED与圆O相切,所以有1个交点
(3)如下图,连接CF
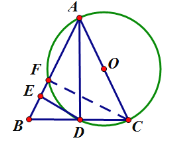
∵AC是圆O的直径,∴∠AFC=90°
又∵∠DEB=90°,∴DE∥CF
∵AB=AC,AD⊥BC,∴BD=DC
∴DE是△BCF的中位线
∵BE=1,∴EF=1
∵cos∠BAC=![]()
∴在Rt△ACF中,设AF=3x,则AC=5x,
∴AB=5x,∴BF=2x=2,∴x=1
∴AF=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=
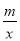 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.(1)求m的值和点B的坐标;
(2)点P在双曲线y=
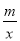 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出口
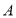 ,
,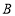 ,
,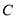 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中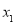 ,
,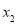 ,
,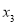 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段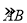 ,
,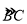 ,
,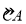 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).(1)若
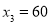 ,
,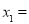 __________.
__________.(2)
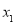 与
与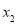 的等量关系为__________.
的等量关系为__________.(3)
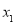 ,
,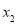 ,
,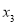 的大小关系为__________.(用>连接).
的大小关系为__________.(用>连接).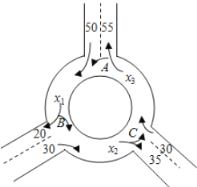
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
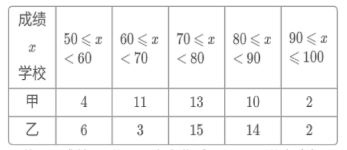
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x
学校

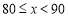

甲
4
11
13
10
2
乙
6
3
15
14
2
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在
 这一组的是:
这一组的是:70 70 70 71 72 73 73 73 74 75 76 77 78
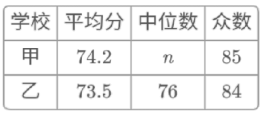
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校
平均分
中位数
众数
甲
74.2
n
5
乙
73.5
76
84
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
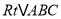 中,
中,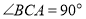 ,
,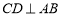 于点
于点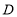 ,
,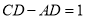 ,为了研究图中线段之间的关系,设
,为了研究图中线段之间的关系,设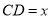 ,
,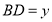 ,
,(1)可通过证明
 ,得到
,得到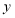 关于
关于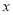 的函数表达式
的函数表达式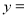 __________,其中自变量
__________,其中自变量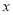 的取值范围是___________;
的取值范围是___________;(2)根据图中给出的(1)中函数图象上的点,画出该函数的图象;
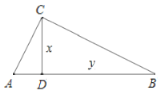

(3)借助函数图象,回答下列问题:①
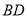 的最小值是__________;②已知当
的最小值是__________;②已知当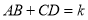 时,
时,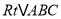 的形状与大小唯一确定,借助函数图象给出
的形状与大小唯一确定,借助函数图象给出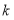 的一个估计值(精确到0.1)或者借助计算给出
的一个估计值(精确到0.1)或者借助计算给出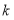 的精确值.
的精确值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
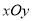 中,抛物线
中,抛物线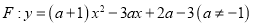
(1)当
 时,求抛物线
时,求抛物线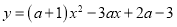 的顶点坐标;
的顶点坐标;(2)已知点
 ,抛物线
,抛物线 与
与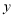 轴交于点
轴交于点 (不与
(不与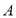 重合),将点
重合),将点 绕点
绕点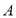 逆时针旋转90°至点
逆时针旋转90°至点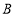 ,
,①直接写出点
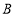 的坐标(用含
的坐标(用含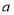 的代数式表示);
的代数式表示);②若抛物线
 与线段
与线段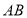 有且仅有一个公共点,求
有且仅有一个公共点,求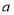 的取值范围.
的取值范围. -
科目: 来源: 题型:
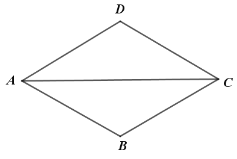
查看答案和解析>>【题目】如图,四边形
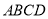 是菱形,且
是菱形,且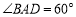 ,点
,点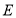 是对角线
是对角线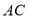 上一点,
上一点,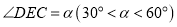 ,绕点
,绕点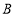 逆时针旋转射线
逆时针旋转射线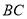 ,旋转角度为
,旋转角度为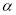 ,并交射线
,并交射线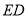 于点
于点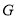 ,连接
,连接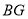 ,
,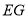 ,
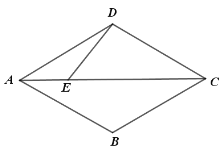
,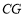 ,
,
(1)①当
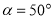 时,补全图形,并证明
时,补全图形,并证明 ;
;
②当
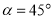 时,直接写出线段
时,直接写出线段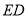 ,
,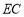 ,
,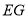 之间的关系;
之间的关系;(2)在平面上找到一点
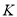 ,使得对于任意的
,使得对于任意的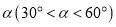 ,总有
,总有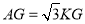 ,直接写出点
,直接写出点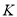 的位置.
的位置.(3)选择下面任意一问回答即可(全卷最多不超过100分)
A.证明(1)②的结论.
B.根据(2)中找到的
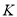 的位置,证明
的位置,证明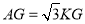
相关试题

