【题目】在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,sin∠EMP= ![]() .
.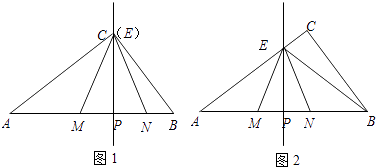
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A,C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出x的取值范围;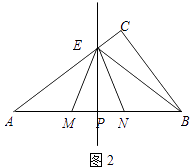
(3)若△AME∽△ENB,求AP的长.
参考答案:
【答案】
(1)
解:∵∠ACB=90°,
∴AC= ![]() =
= ![]() =40,
=40,
∵CP⊥AB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CP=24,
∴CM= ![]() =
= ![]() =26
=26
(2)
解:∵sin∠EMP= ![]() ,
,
∴设EP=12a,
则EM=13a,PM=5a,
∵EM=EN,
∴EN=13a,PN=5a,
∵△AEP∽△ABC,
∴ ![]() ,
,
∴ ![]() =
= ![]()
∴x=16a,
∴a= ![]() ,
,
∴BP=50﹣16a,
∴y=50﹣21a,
=50﹣21× ![]() ,
,
=50﹣ ![]() x,
x,
∵当E点与A点重合时,x=0.当E点与C点重合时,x=32.
∴函数的定义域是:(0<x<32)
(3)
解:①当点E在AC上时,如图2,
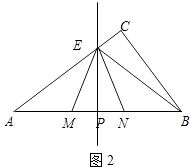
设EP=12a,则EM=13a,MP=NP=5a,
∵△AEP∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AP=16a,
∴AM=11a,
∴BN=50﹣16a﹣5a=50﹣21a,
∵△AME∽△ENB,
∴ ![]() =
= ![]()
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
∴AP=16× ![]() =22,
=22,
②当点E在BC上时,如图(备用图),设EP=12a,则EM=13a,MP=NP=5a,
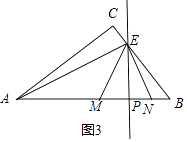
∵△EBP∽△ABC,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得BP=9a,
∴BN=9a﹣5a=4a,AM=50﹣9a﹣5a=50﹣14a,
∵△AME∽△ENB,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得a= ![]() ,
,
∴AP=50﹣9a=50﹣9× ![]() =42.
=42.
所以AP的长为:22或42.
【解析】((1)本题需先根据已知条件得出AC的值,再根据CP⊥AB求出CP,从而得出CM的值.(2)本题需先根据EN,根据sin∠EMP= ![]() ,设出EP的值,从而得出EM和PM的值,再得出△AEP∽△ABC,即可求出
,设出EP的值,从而得出EM和PM的值,再得出△AEP∽△ABC,即可求出 ![]() =
= ![]() ,求出a的值,即可得出y关于x的函数关系式,并且能求出函数的定义域.(3)本题需先设EP的值,得出则EM和MP的值,然后分①点E在AC上时,根据△AEP∽△ABC,求出AP的值,从而得出AM和BN的值,再根据△AME∽△ENB,求出a的值,得出AP的长;②点E在BC上时,根据△EBP∽△ABCC,求出AP的值,从而得出AM和BN的值,再根据△AME∽△ENB,求出a的值,得出AP的长.
,求出a的值,即可得出y关于x的函数关系式,并且能求出函数的定义域.(3)本题需先设EP的值,得出则EM和MP的值,然后分①点E在AC上时,根据△AEP∽△ABC,求出AP的值,从而得出AM和BN的值,再根据△AME∽△ENB,求出a的值,得出AP的长;②点E在BC上时,根据△EBP∽△ABCC,求出AP的值,从而得出AM和BN的值,再根据△AME∽△ENB,求出a的值,得出AP的长.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的顶点为(1,0),且经过点(0,1).
(1)求该抛物线对应的函数的解析式;
(2)将该抛物线向下平移m(m>0)个单位,设得到的抛物线的顶点为A,与x轴的两个交点为B、C,若△ABC为等边三角形.
①求m的值;
②设点A关于x轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP为菱形?若存在,写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的运算流程中,
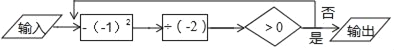
(1)若输入的数x=﹣4,则输出的数y= ;
(2)若输出的数y=5,则输入的数x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(
 ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是
 ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题.
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?

相关试题

