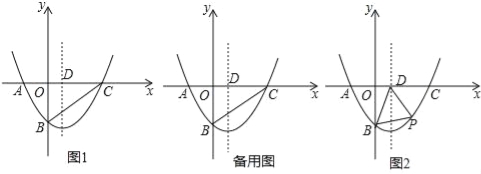
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)(8﹣2
x﹣4;(2)(8﹣2![]() ,﹣
,﹣![]() )、(0,﹣4)、(
)、(0,﹣4)、(![]() ,﹣
,﹣![]() );(3)(
);(3)(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)∵二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,∴![]() ,解得
,解得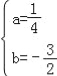 ,∴该二次函数的解析式为y=
,∴该二次函数的解析式为y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)由二次函数y=![]() x2﹣
x2﹣![]() x﹣4可知对称轴x=3,∴D(3,0),∵C(8,0),∴CD=5,由二次函数y=
x﹣4可知对称轴x=3,∴D(3,0),∵C(8,0),∴CD=5,由二次函数y=![]() x2﹣
x2﹣![]() x﹣4可知B(0,﹣4),设直线BC的解析式为y=kx+b,∴
x﹣4可知B(0,﹣4),设直线BC的解析式为y=kx+b,∴![]() ,解得
,解得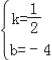 ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x﹣4,设E(m,
x﹣4,设E(m,![]() m﹣4),当DC=CE时,EC2=(m﹣8)2+(
m﹣4),当DC=CE时,EC2=(m﹣8)2+(![]() m﹣4)2=CD2,即(m﹣8)2+(
m﹣4)2=CD2,即(m﹣8)2+(![]() m﹣4)2=52,解得m1=8﹣2
m﹣4)2=52,解得m1=8﹣2![]() ,m2=8+2
,m2=8+2![]() (舍去),∴E(8﹣2
(舍去),∴E(8﹣2![]() ,﹣
,﹣![]() );当DC=DE时,ED2=(m﹣3)2+(
);当DC=DE时,ED2=(m﹣3)2+(![]() m﹣4)2=CD2,即(m﹣3)2+(
m﹣4)2=CD2,即(m﹣3)2+(![]() m﹣4)2=52,解得m3=0,m4=8(舍去),∴E(0,﹣4);当EC=DE时,(m﹣8)2+(
m﹣4)2=52,解得m3=0,m4=8(舍去),∴E(0,﹣4);当EC=DE时,(m﹣8)2+(![]() m﹣4)2=(m﹣3)2+(
m﹣4)2=(m﹣3)2+(![]() m﹣4)2解得m5=5.5,∴E(
m﹣4)2解得m5=5.5,∴E(![]() ,﹣
,﹣![]() ).综上,存在点E,使得△CDE为等腰三角形,所有符合条件的点E的坐标为(8﹣2
).综上,存在点E,使得△CDE为等腰三角形,所有符合条件的点E的坐标为(8﹣2![]() ,﹣
,﹣![]() )、(0,﹣4)、(
)、(0,﹣4)、(![]() ,﹣
,﹣![]() ).
).
(3)过点P作y轴的平行线交x轴于点F,∵P点的横坐标为m,∴P点的纵坐标为![]() m2﹣
m2﹣![]() m﹣4,∵△PBD的面积S=S梯形﹣S△BOD﹣S△PFD=
m﹣4,∵△PBD的面积S=S梯形﹣S△BOD﹣S△PFD=![]() m[4﹣(
m[4﹣(![]() m2﹣
m2﹣![]() m﹣4)]﹣
m﹣4)]﹣![]() (m﹣3)[﹣(
(m﹣3)[﹣(![]() m2﹣
m2﹣![]() m﹣4)]﹣
m﹣4)]﹣![]() ×3×4=﹣
×3×4=﹣![]() m2+
m2+![]() m=﹣
m=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,∴当m=
,∴当m=![]() 时,△PBD的最大面积为
时,△PBD的最大面积为![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛,他收集了小明、小白近期10次数学考试成绩,并绘制了折线统计图(如图所示)
项目
众数
中位数
平均数
方差
最高分
小明
85
85
小白
70,100
85
100
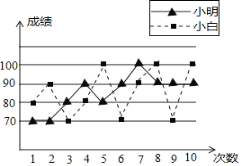
(1)根据折线统计图,张老师绘制了不完整的统计表,请你补充完整统计表;
(2)你认为张老师会选择哪位同学参加比赛?并说明你的理由
-
科目: 来源: 题型:
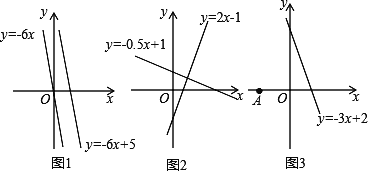
查看答案和解析>>【题目】材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:在直线L1:y=K1x+b1与直线L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:在直线L1:y=k1x+b1 与L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反过来,也成立
应用举例
已知直线y=﹣
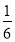 x+5与直线y=kx+2互相垂直,则﹣
x+5与直线y=kx+2互相垂直,则﹣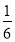 k=﹣1.所以k=6
k=﹣1.所以k=6解决问题
(1)请写出一条直线解析式______,使它与直线y=x﹣3平行.
(2)如图3,点A坐标为(﹣1,0),点P是直线y=﹣3x+2上一动点,当点P运动到何位置时,线段PA的长度最小?并求出此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
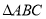 中,
中,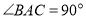 ,
,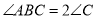 ,
,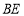 平分
平分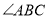 交于点
交于点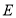 ,
,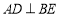 于点
于点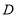 ,下列结论:①
,下列结论:①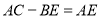 ;②
;②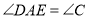 ;③
;③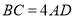 ;④点
;④点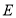 在线段
在线段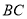 的垂直平分线上,其中正确的个数有( )
的垂直平分线上,其中正确的个数有( )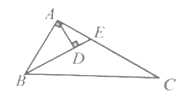
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点.
(1)若AC=4,BC=6,求CF的长.
(2)若AB=16CF,求
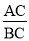 的值.
的值.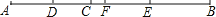
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
相关试题

