【题目】如图,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点.
(1)若AC=4,BC=6,求CF的长.
(2)若AB=16CF,求![]() 的值.
的值.
![]()
参考答案:
【答案】(1)CF=![]() ;(2)
;(2)![]() =
=![]() 或
或![]() .
.
【解析】
(1)根据线段的中点定义求出DF的长,再根据线段的和差即可求解;
(2)分两种情况画图,再根据线段中点定义即可求解.
解:(1)∵D为AC的中点,
∴AD=CD=![]() AC=2
AC=2
∵E为BC中点,
∴CE=BE=![]() BC=3
BC=3
∴DE=DC+CE=5
∵F为DE中点
∴DF=![]() DE=
DE=![]()
∴CF=DF﹣DC=![]() ﹣2=
﹣2=![]()
(2)当F在C点右侧时,
如图:![]()
设AD=CD=x,CE=BE=y,
则DF=![]() DE=
DE=![]() (x+y)
(x+y)
∴CF=DF﹣DC=![]() (y﹣x)
(y﹣x)
∴由AB=16CF得:2(x+y)=8(y﹣x),
∴5x=3y
∴![]()
②当F在C点的左侧时,
如图:![]()
CF=DC﹣DF=![]() (x﹣y)
(x﹣y)
2(x+y)=16×![]() (x﹣y)
(x﹣y)
∴5x=3y,
∴![]() =
=![]() =
=![]()
综上:![]() =
=![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
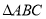 中,
中,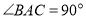 ,
,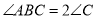 ,
,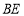 平分
平分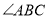 交于点
交于点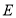 ,
,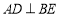 于点
于点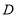 ,下列结论:①
,下列结论:①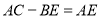 ;②
;②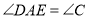 ;③
;③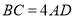 ;④点
;④点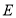 在线段
在线段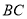 的垂直平分线上,其中正确的个数有( )
的垂直平分线上,其中正确的个数有( )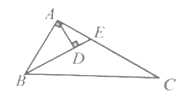
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
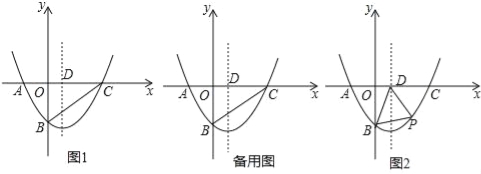
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E是边CD上一点,将△ADE沿AE折叠至
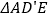 处,
处,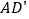 与CE交于点F,若∠B=52°,∠DAE=20°,则
与CE交于点F,若∠B=52°,∠DAE=20°,则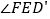 的度数为( )
的度数为( )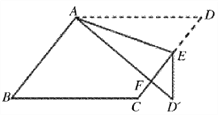
A. 40° B. 36° C. 50° D. 45°
相关试题

