【题目】如图,已知![]() 为
为![]() 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.
(1)作![]() 的平分线
的平分线![]() .
.
(2)在![]() 上取一点
上取一点![]() ,使得
,使得![]() .
.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,这时他发现
,这时他发现![]() 与
与![]() 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

参考答案:
【答案】(1)答案见解析;(2)答案见解析;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)以点O为圆心,以任意长为半径画弧与∠AOB的两边分别相交,再以两交点为圆心,以大于两交点之间的距离的一半为半径画弧,相交于一点,过这一点与O作射线OC即可;
(2)在OC上取一点P,使得OP=a;
(3)以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,PN⊥OB于N,根据角平分线上的点到角的两边的距离相等可得PM=PN,利用HL证明△E2PM≌△DPN,得出∠OE2P=∠ODP,再根据平角的定义即可求解.
试题解析:(1)如图,OC即为所求;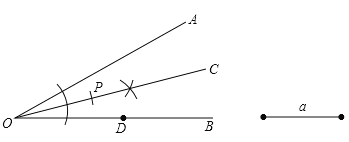
(2)如图,OP=a;
(3)∠OEP=∠ODP或∠OEP+∠ODP=180°.
理由是:以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,
PN⊥OB于N,则PM=PN.
在△E2PM和△DPN中,![]() ,
,
∴△E2PM≌△DPN(HL),
∴∠OE2P=∠ODP;
以P为圆心,以PD为半径作弧,交OA于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
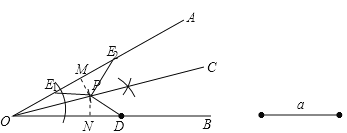
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
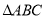 中,
中,  是
是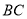 边上的点,将
边上的点,将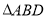 绕点
绕点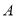 旋转,得到
旋转,得到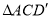 .
.(1)当
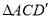 时,求证:
时,求证: 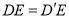 .
.(2)在(1)的条件下,猜想
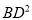 ,
, 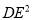 ,
, 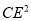 有怎样的数量关系,并说明理由.
有怎样的数量关系,并说明理由.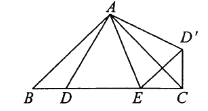
-
科目: 来源: 题型:
查看答案和解析>>【题目】三门湾核电站的1号机组将于2013年的10月建成,其功率将达到1 250 000千瓦.其中1 250 000可用科学记数法表示为( )
A.125×104
B.12.5×105
C.1.25×106
D.0.125×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】a5 可以等于( )
A. (-a)2·(-a)3B. (-a) ·(-a)4C. (-a 2) ·a 3D. (-a 3) ·(-a 2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别为81 cm2和144 cm2,则正方形③的边长为( )

A. 225 cm B. 63 cm C. 50 cm D. 15 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学测试的平均成绩为80分.如果小田考93分记作+13分,那么小润考76分记作 分,小红考80分记作 分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算
 的近似值.
的近似值.小明的方法:
∵
 <
< <
< ,
,设
 =3+k(0<k<1).
=3+k(0<k<1).∴
 .
.∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈
 .
.∴
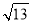 ≈3+
≈3+ ≈3.67.
≈3.67.问题:
(1)请你依照小明的方法,估算
 的近似值;
的近似值;(2)请结合上述具体实例,概括出估算
 的公式:已知非负整数a、b、m,若a<
的公式:已知非负整数a、b、m,若a< <a+1,且m=a2+b,则
<a+1,且m=a2+b,则 ≈ (用含a、b的代数式表示);
≈ (用含a、b的代数式表示);(3)请用(2)中的结论估算
 的近似值.
的近似值.
相关试题

