【题目】已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别为81 cm2和144 cm2,则正方形③的边长为( )

A. 225 cm B. 63 cm C. 50 cm D. 15 cm
参考答案:
【答案】D
【解析】试题解析:∵四边形①、②、③都是正方形,
∴∠EAB=∠EBD=∠BCD=90°,BE=BD,
∴∠AEB+∠ABE=90°,∠ABE+∠DBC=90°,
∴∠AEB=∠CBD.
在△ABE和△CDB中, ,
,
∴△ABE≌△CDB(AAS),
∴AE=BC,AB=CD.
∵正方形①、②的面积分别81cm2和144cm2,
∴AE2=81,CD2=144.
∴AB2=63.
在Rt△ABE中,由勾股定理,得
BE2=AE2+AB2=81+144=225,
∴BE=15.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三门湾核电站的1号机组将于2013年的10月建成,其功率将达到1 250 000千瓦.其中1 250 000可用科学记数法表示为( )
A.125×104
B.12.5×105
C.1.25×106
D.0.125×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】a5 可以等于( )
A. (-a)2·(-a)3B. (-a) ·(-a)4C. (-a 2) ·a 3D. (-a 3) ·(-a 2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 为
为 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.(1)作
 的平分线
的平分线 .
.(2)在
 上取一点
上取一点 ,使得
,使得 .
.(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
 上取一点
上取一点 ,使得
,使得 ,这时他发现
,这时他发现 与
与 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学测试的平均成绩为80分.如果小田考93分记作+13分,那么小润考76分记作 分,小红考80分记作 分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算
 的近似值.
的近似值.小明的方法:
∵
 <
< <
< ,
,设
 =3+k(0<k<1).
=3+k(0<k<1).∴
 .
.∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈
 .
.∴
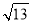 ≈3+
≈3+ ≈3.67.
≈3.67.问题:
(1)请你依照小明的方法,估算
 的近似值;
的近似值;(2)请结合上述具体实例,概括出估算
 的公式:已知非负整数a、b、m,若a<
的公式:已知非负整数a、b、m,若a< <a+1,且m=a2+b,则
<a+1,且m=a2+b,则 ≈ (用含a、b的代数式表示);
≈ (用含a、b的代数式表示);(3)请用(2)中的结论估算
 的近似值.
的近似值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一家化工厂原来每月利润为120万元,从今年1月起安装使用回收净化设备(安装时间不计),一方面改善了环境,另一方面大大降低原料成本.据测算,使用回收净化设备后的1至x月(1≤x≤12)的利润的月平均值w(万元)满足w=10x+90,第二年的月利润稳定在第1年的第12个月的水平.
(1)设使用回收净化设备后的1至x月(1≤x≤12)的利润和为y,写出y关于x的函数关系式,并求前几个月的利润和等于700万元;
(2)当x为何值时,使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等;
(3)求使用回收净化设备后两年的利润总和.
相关试题

